Так как дополнительные краевые условия аналогичны предыдущему примеру, вновь имеем 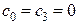 , но, учитывая, что
, но, учитывая, что 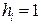 составим систему (56):
составим систему (56):
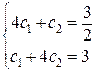
Решение этой системы будет
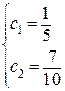
Значения коэффициентов 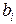 ,
, 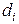 :
:
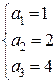
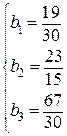

Таким образом, можно считать сплайн-интерполяцию построенной в виде
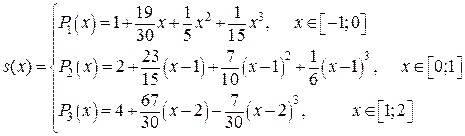
Для нахождения значения интерполирующей функции в заданной точке 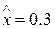 заметим, что
заметим, что 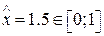 , и поэтому используем многочлен
, и поэтому используем многочлен 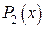 :
: 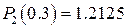 .
.
|

Сравнивая примеры 7 и 8 обратим внимание на следующее: погрешность в последнем явно меньше. Связано это в первую очередь с тем, что интервал выбран в два раза меньше. Можно показать, для случая равноотстоящих узлов
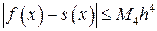
где 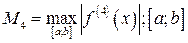 - промежуток интерполяции.
- промежуток интерполяции.
Интерполяция сплайнами сопряжена с немалым объемом вычислительной работы по сравнению с другими видами интерполяции. Однако эта трудность легко решается с помощью ЭВМ.
Контрольные вопросы и задачи
1. Дать определение истинной абсолютной и предельной абсолютной погрешностей приближенного числа. В чем их различие?
2. Найти предельную абсолютную погрешность числа 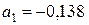 числом
числом 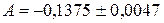 .
.
3. Дать определение истинной относительной и предельной относительной погрешностей приближенного числа. В чем их различие?
4. Вывести формулу для определения предельной относительной погрешности приближенного числа.
5. Найти предельную относительную погрешность числа 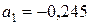 числом
числом 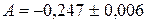 .
.
6. Выяснить, какое из приближенных равенств точнее: 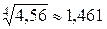 или
или 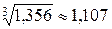 .
.
7. Дать понятие значащей, верной цифр числа.
8. Записать число a=104,7032 в виде позиционной записи. Найти старший и младший разряды.
9. В числе 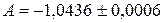 найти верные цифры. Округлить приближенное число с сохранением верных цифр.
найти верные цифры. Округлить приближенное число с сохранением верных цифр.
10. Вывести формулу для вычисления предельной абсолютной погрешности суммы (разности) двух приближенных чисел.
11. Даны числа 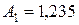 ;
; 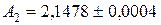 ;
; 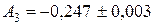 . Найти приближение
. Найти приближение 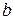 для точного числа
для точного числа 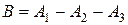 . Вычислить погрешности; результат
. Вычислить погрешности; результат 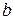 округлить с сохранением верных цифр.
округлить с сохранением верных цифр.
12. Вывести формулы для вычисления предельной абсолютной и предельной относительной погрешностей произведения (частного) двух приближенных чисел.
13. Чему равны 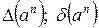 .
.
14. Дано число 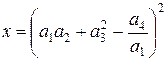 . Выразить
. Выразить 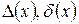 через числа
через числа 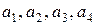 и их предельные абсолютные погрешности.
и их предельные абсолютные погрешности.
15. Пусть 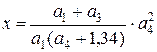 . Выразить
. Выразить 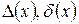 через
через 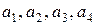 и их предельные абсолютные погрешности.
и их предельные абсолютные погрешности.
16. Вывести формулы для вычисления предельной абсолютной и предельной относительной погрешностей значения функции в точке.
17. Вывести формулы для вычисления предельной абсолютной и предельной относительной погрешностей значений основных элементарных функций.
18. Дать алгоритм табулирования функции на заданном отрезке с заданным шагом.
19. Построить квадратичную интерполяцию Лагранжа, сплайн-интерполяцию и график функции 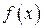 на отрезке
на отрезке 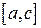 по трем ее значениям:
по трем ее значениям: 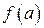 ,
, 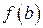 ,
, 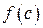 . Найти остаточный член, оценить погрешность интерполяции по контрольной точке
. Найти остаточный член, оценить погрешность интерполяции по контрольной точке 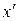 и сравнить ее с фактической (по таблицам).
и сравнить ее с фактической (по таблицам).
| № | 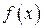
| 
| 
| 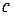
| 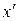
| № | 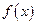
| 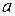
| 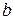
| 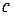
| 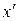
|
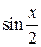
| p/2 | p | p/10 | 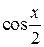
| p/2 | p | p/10 | ||||
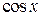
| p/4 | p/2 | p/10 | 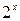
| 2.5 | ||||||
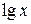
| 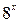
| 2.5 | |||||||||
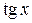
| p/4 | p/3 | p/6 | 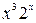
| 2.5 | ||||||
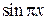
| 1/2 | 1/10 | 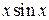
| p/4 | p/3 | p/6 | |||||
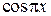
| 1/2 | 1/10 | 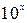
| 2.5 | |||||||
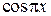
| 1/5 | 1/3 | 2/3 | 1/4 | 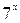
| 2.5 | |||||
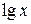
| 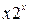
| 2.5 | |||||||||
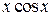
| p/4 | p/3 | p/6 | 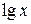
| |||||||
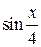
| p | 2p | p/8 | 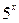
| 2.5 | ||||||
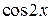
| p/4 | p/2 | p/8 | 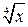
| 2.5 | ||||||
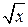
| 2.5 | 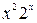
| 4.5 | ||||||||
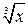
| 2.5 | 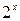
| 2.5 | ||||||||
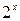
| 2.5 | 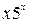
| 2.5 | ||||||||
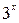
| 2.5 | 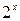
| 5.5 |
21. Найдите многочлен, данные о котором представлены следующей таблицей:
| № | x | 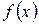
| 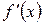
| 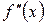
| № | x | 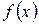
| 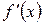
| 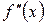
|
| 1. | 16. | ||||||||
| № | x | 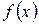
| 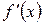
| 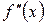
| № | x | 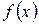
| 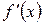
| 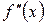
|
Литература
1. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения): Учеб. пособие для вузов. - М.:Высш. шк., 2001.-382 с.
2. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. – М.: «Наука», 1965,-424 с.
3. Смирнов В.И. Курс высшей математики. т.2. – М.: «Наука», 1967.
4. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. – М.: Физматгиз, 1962.
5. Косарев В.И. 12 лекций по вычислительной математике. – М.: Изд-во МФТИ, 1995.
6. Краскевич В.Е. Численные методы в инженерных исследованиях. – Киев: Вища школа, 1986.
7. Бронштейн И.Н., Семендяев К.А.. Справочник по математике для инженеров и учащихся втузов.-М.: «Наука»,1986.-544 с. 
Учебное издание
Александр Борисович Дюбуа,
Светлана Николаевна Машнина
Сергей Александрович Нелюхин
Математический анализ: элементы теории погрешностей и полиномиальные интерполяции
Учебное пособие
Ответственный редактор Н. К. Кадуцков
Компьютерный набор и верстка
А. М. Казакова
Подписано в печать 03.09.2010 г.
Формат 60x84 1/16. Гарнитура «Times New Roman».
Усл. печ. л.4,7. Уч.-изд. л.3,75. Тираж 50 экз.
Отпечатано с готовых диапозитивов
В ООО фирма «Интермета»
г. Рязань, ул. Семинарская, 5, т. 25-81-76

[1] Термины «интерполяция» и «экстраполяция», впервые предложены в 1656 году английским математиком Джоном Уоллисом (J. Wallis), образованы от латинского “polire” – сглаживать, и различаются предлогами “inter” и “extra” – соответственно «между» и «внутри».
[2] Можно показать непосредственную связь между конечными разностями и производными, а именно. Доказательство этого положения предоставляем читателю.
[3] Легко убедиться, что форма будет единственной, обращающейся в нуль в узловых точках.
 2015-04-23
2015-04-23 653
653
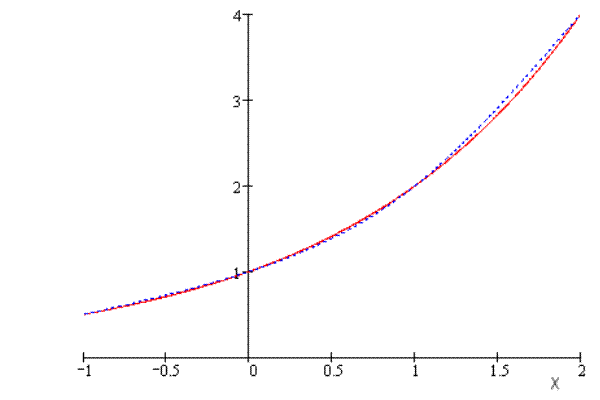 Рис. 3 График функции
Рис. 3 График функции 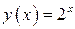 (сплошная кривая) и интерполирующий ее сплайн (пунктирная кривая).
(сплошная кривая) и интерполирующий ее сплайн (пунктирная кривая).







