Неравенство Чебышева

Неравенство Чебышева, используемое для доказательства дальнейших теорем, справедливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.

Теорема (неравенство Чебышева). p( | X – M (X)| < ε) ≥ D (X) / ε². (13.1)

Доказательство. Пусть Х задается рядом распределения

Х	х 1	х 2	…	хп
р	р 1	р 2	…	рп

Так как события | X – M (X)| < ε и | X – M (X)| ≥ ε противоположны,

то р (| X – M (X)| < ε) + + р (| X – M (X)| ≥ ε) = 1, следовательно, р (| X – M (X)| < ε) = 1 - р (| X – M (X)| ≥ ε). Найдем р (| X – M (X)| ≥ ε).

D (X) = (x ₁ – M (X))² p ₁ + (x ₂ – M (X))² p ₂ + … + (x_n – M (X))² p_n. Исключим из этой суммы те слагаемые, для которых | X – M (X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых.

Тогда D (X) ≥ (x_{k+ 1} – M (X))² p_{k+ 1} + (x_{k+ 2} – M (X))² p_{k +2} + … + (x_n – M (X))² p_n ≥ ε² (p_{k+ 1} + p_{k+ 2} + … + p_n).

Отметим, что p_{k+ 1} + p_{k+ 2} + … + p_n есть вероятность того, что | X – M (X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо.

Следовательно, D (X) ≥ ε² р (| X – M (X)| ≥ ε), или р (| X – M (X)| ≥ ε) ≤ D (X) / ε².

Тогда вероятность противоположного события p( | X – M (X)| < ε) ≥ D (X) / ε², что и требовалось доказать.

Тема 21, 22, 22.

Теорема Чебышева. Обобщённая теорема. Теорема Маркова.

В формулировке ЗБЧ используется понятие «сходимости случайных величин по вероятности».

Последовательность случайных величин ξ ₁, ξ ₂,…,ξ _n сходится по вероятности к величине a (случайной или неслучайной), если для любого ε > 0 вероятность события |ξ_n – a| < ε при n → ∞ стремится к единице: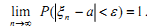

Теорема Чебышева

Частным случаем закона больших чисел является теорема Бернулли.

Теоремы Чебышева и Бернулли.

Теорема 13.2 (теорема Чебышева). Если Х ₁, Х ₂,…, Х_п – попарно независимые случайные величины, дисперсии которых равномерно ограничены (D (X_i) ≤ C), то для сколь угодно малого числа ε вероятность неравенства

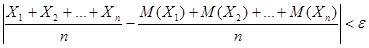
будет сколь угодно близка к 1, если число случайных величин достаточно велико.

Замечание. Иначе говоря, при выполнении этих условий

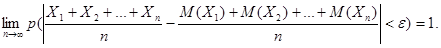
Доказательство. Рассмотрим новую случайную величину 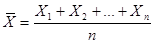и найдем ее математическое ожидание. Используя свойства математического ожидания, получим, что 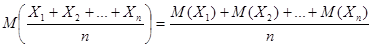. Применим к 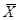неравенство Чебышева: 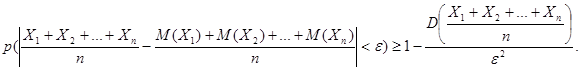Так как рассматриваемые случайные величины независимы, то, учитывая условие теоремы, имеем: 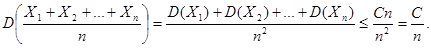Используя этот результат, представим предыдущее неравенство в виде:

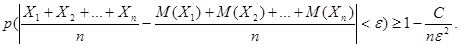Перейдем к пределу при 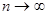: 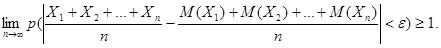Поскольку вероятность не может быть больше 1, можно утверждать, что

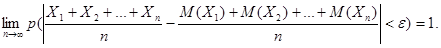Теорема доказана.

Следствие.

Если Х ₁, Х ₂, …, Х_п – попарно независимые случайные величины с равномерно ограничен-ными дисперсиями, имеющие одинаковое математическое ожидание, равное а, то для любого сколь угодно малого ε > 0 вероятность неравенства 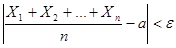будет как угодно близка к 1, если число случайных величин достаточно велико. Иначе говоря, .

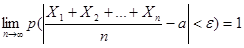Вывод: среднее арифметическое достаточно большого числа случайных величин прини-мает значения, близкие к сумме их математических ожиданий, то есть утрачивает характер случайной величины. Например, если проводится серия измерений какой-либо физической величины, причем: а) результат каждого измерения не зависит от результатов остальных, то есть все результаты представляют собой попарно независимые случайные величины; б) измерения производятся без систематических ошибок (их математические ожидания равны между собой и равны истинному значению а измеряемой величины); в) обеспечена определенная точность измерений, следовательно, дисперсии рассматривае-мых случайных величин равномерно ограничены; то при достаточно большом числе измерений их среднее арифметическое окажется сколь угодно близким к истинному значению измеряемой величины.