Частным случаем функциональных рядов являются степенные ряды.
Определение Степенным рядом называется функциональный ряд
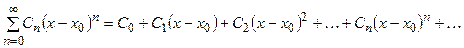 ,
,
члены которого являются произведениями постоянных 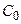 ,
, 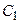 ,...,
,..., 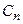 ,... на степенные функции от разности
,... на степенные функции от разности 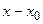 с целыми неотрицательными показателями степеней, точка x0 называется центром степенного ряда.
с целыми неотрицательными показателями степеней, точка x0 называется центром степенного ряда.
Пример 19. Ряд 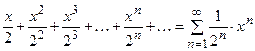 – степенной ряд с центром в точке
– степенной ряд с центром в точке 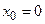 .
.
Ряд 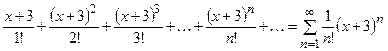 – степенной ряд с центром в точке
– степенной ряд с центром в точке 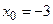 .
.
Ряд 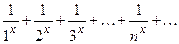 – функциональный ряд.
– функциональный ряд.
Исследование степенного ряда на сходимость, а именно нахождение области сходимости степенного ряда, является одним из главных вопросов. Решение этого вопроса связано с теоремой Абеля.
Теорема (Абеля)
1 Если степенной ряд сходится при 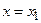
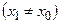 , то он сходится, и притом абсолютно, для всех
, то он сходится, и притом абсолютно, для всех 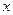 , удовлетворяющих неравенству
, удовлетворяющих неравенству
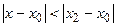 .
.
2 Если степенной ряд расходится при 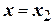 , то он расходится для всех
, то он расходится для всех 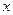 , удовлетворяющих неравенству
, удовлетворяющих неравенству
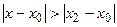 .
.
 2015-04-23
2015-04-23 422
422








