Определение. Числовой ряд называется знакочередующимся, если его члены поочередно меняют знак. Знакочередующийся ряд можно записать в виде
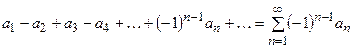
где 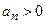 .
.
Для знакочередующихся рядов имеет место следующий очень простой достаточный признак сходимости.
Теорема (Признак Лейбница)
Если для знакочередующегося ряда все его члены удовлетворяют условиям:
а) 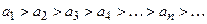 (т.е. члены ряда монотонно убывают по абсолютной величине);
(т.е. члены ряда монотонно убывают по абсолютной величине);
б) 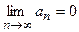 (т.е. общий член ряда стремится к нулю при
(т.е. общий член ряда стремится к нулю при 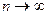 ), то такой ряд сходится, а его сумма не превосходит первого члена.
), то такой ряд сходится, а его сумма не превосходит первого члена.
Ряд, удовлетворяющий условиям данной теоремы, называют рядом Лейбница.
Пример 14. Исследовать сходимость ряда 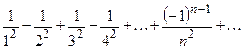 по признаку Лейбница.
по признаку Лейбница.
Данный знакочередующийся ряд сходится, так как удовлетворяет условиям признака Лейбница:
а) 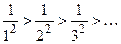 ;
;
б) 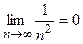 .
.
Пример 15. Исследовать сходимость ряда 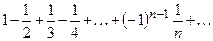
Данный знакочередующийся ряд сходится, так как удовлетворяет условиям признака Лейбница:
а) 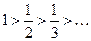 ;
;
б) 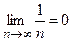 .
.
Заметим, что данный ряд отличается от гармонического только знаками четных членов.
 2015-04-23
2015-04-23 653
653








