Если степенной ряд сходится в точке 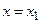 , то он сходится и во всех точках, расположенных ближе к центру степенного ряда
, то он сходится и во всех точках, расположенных ближе к центру степенного ряда 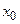 , чем
, чем 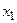 . Если же ряд расходится при
. Если же ряд расходится при 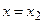 , то он расходится и во всех более удаленных от центра ряда точках.
, то он расходится и во всех более удаленных от центра ряда точках.
Опираясь на теорему Абеля можно доказать, что существует такое положительное число 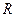 , что для всех
, что для всех 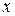 , удовлетворяющих неравенству
, удовлетворяющих неравенству 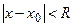 , ряд сходится абсолютно и расходится при всех
, ряд сходится абсолютно и расходится при всех 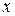 , для которых
, для которых 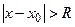 .
.
Число 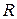 называется радиусом сходимости ряда
называется радиусом сходимости ряда 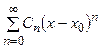 , а интервал
, а интервал 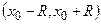 – интервалом сходимости.
– интервалом сходимости.

В частном случае интервал сходимости степенного ряда может совпадать со всей числовой осью (в этом случае 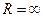 ) или может превращаться в точку (в этом случае
) или может превращаться в точку (в этом случае 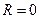 ). Заметим, что интервал сходимости всегда симметричен относительно центра степенного ряда.
). Заметим, что интервал сходимости всегда симметричен относительно центра степенного ряда.
Если для степенного ряда существует 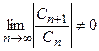 , то радиус сходимости степенного ряда можно вычислить по формуле
, то радиус сходимости степенного ряда можно вычислить по формуле
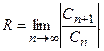
Рассмотрим способы определения области сходимости степенного ряда на примерах.
Пример 20. Найти интервал сходимости степенного ряда 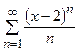 .
.
 2015-04-23
2015-04-23 913
913








