Знакопеременные ряды

Определение. Ряд называется знакопеременным, если он содержит как положительные, так и отрицательные члены.

Пример 15. Ряды

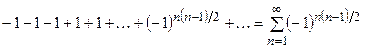
и

, ,

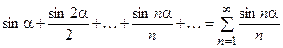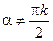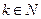
являются знакопеременными.

Знакочередующиеся ряды, очевидно, являются частным случаем знакопеременных рядов. Для знакопеременного ряда 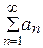возникает вопрос о связи его сходимости со сходимостью знакоположительного ряда .

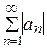Теорема (Признак абсолютной сходимости). Если сходится ряд 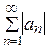, то сходится и ряд .

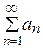Определения. Если сходится ряд 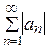, то ряд 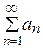называется абсолютно сходящимся. Если же ряд 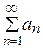сходится, а ряд 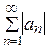расходится, то ряд 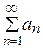называется условно сходящимся.

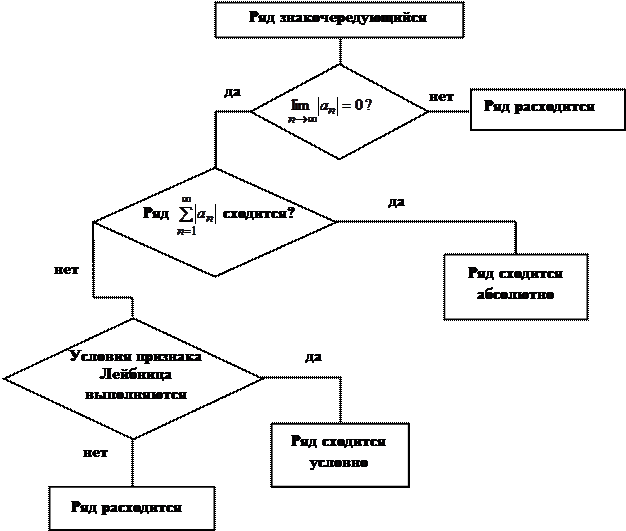
При исследовании знакочередующихся рядов на сходимость можно рассуждать по следующей схеме:

Пример 16. Исследовать на сходимость ряд .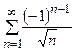

Общий член этого ряда 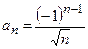. Так как 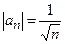, то ряд 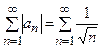расходится, так как является рядом Дирихле, в котором 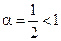. Ряд 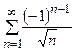согласно признаку Лейбница сходится. Следовательно, исследуемый ряд сходится условно.

Пример 17. Исследовать на сходимость ряд .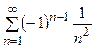

Этот ряд сходится абсолютно, так как ряд 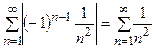– сходящийся ряд Дирихле.

Пример 18. Исследовать на сходимость ряд .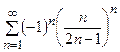

Данный ряд знакочередующийся. Исследуем ряд, составленный из модулей его членов, т.е. ряд 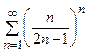. Используя признак Коши, получаем

.

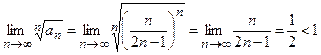Следовательно, данный ряд сходится абсолютно.

Ранее отмечалось, что в знакоположительных рядах можно произвольным образом переставлять и группировать члены. В знакопеременных рядах, если они абсолютно сходятся, это свойство сохраняется. Для условно сходящихся рядов дело обстоит иначе. Здесь группировка, перестановка членов ряда может нарушить сходимость ряда. Например, если из знакочередующегося условно сходящегося ряда выделить положительные члены, то полученный ряд может расходиться. Следует иметь в виду это обстоятельство и с условно сходящимися рядами обращаться с большой осторожностью.