Пусть 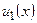 ,
, 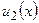 ,...,
,..., 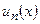 ,...– последовательность функций, определенных на некотором множестве
,...– последовательность функций, определенных на некотором множестве 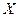 .
.
Определение Ряд вида
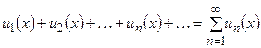 ,
,
членами которого являются функции, называется функциональным.
Придавая 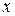 различные числовые значения из множества
различные числовые значения из множества 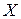 , будем получать различные числовые ряды. В частности, при
, будем получать различные числовые ряды. В частности, при 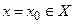 функциональный ряд становится числовым рядом
функциональный ряд становится числовым рядом 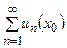 . Этот числовой ряд может быть сходящимся или расходящимся. Если он сходится, то
. Этот числовой ряд может быть сходящимся или расходящимся. Если он сходится, то 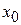 называется точкой сходимости функционального ряда.
называется точкой сходимости функционального ряда.
Множество всех точек сходимости функционального ряда называют его областью сходимости и обозначают ее через 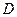 . Очевидно,
. Очевидно, 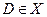 . В частных случаях множество
. В частных случаях множество 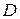 может совпадать или не совпадать с множеством
может совпадать или не совпадать с множеством 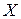 или же может быть и пустым множеством. В последнем случае функциональный ряд расходится в каждой точке множества
или же может быть и пустым множеством. В последнем случае функциональный ряд расходится в каждой точке множества 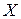 .
.
Вид области 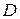 для произвольного функционального ряда может быть различным: вся числовая ось, интервал, объединение интервалов и полуинтервалов и т.д. В простейших случаях при исследовании функциональных рядов на сходимость можно применить рассмотренные выше признаки сходимости числовых рядов, если под x понимать фиксированное число.
для произвольного функционального ряда может быть различным: вся числовая ось, интервал, объединение интервалов и полуинтервалов и т.д. В простейших случаях при исследовании функциональных рядов на сходимость можно применить рассмотренные выше признаки сходимости числовых рядов, если под x понимать фиксированное число.
Определения. Сумма первых 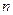 членов функционального ряда
членов функционального ряда 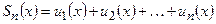 называется
называется 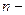 ой частичной суммой, а функция
ой частичной суммой, а функция 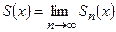 , определенная в области
, определенная в области 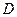 ,– суммой функционального ряда. Функция
,– суммой функционального ряда. Функция 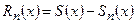 , определенная в области
, определенная в области 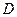 , называется остатком ряда. Функциональный ряд называется абсолютно сходящимся на множестве
, называется остатком ряда. Функциональный ряд называется абсолютно сходящимся на множестве 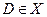 , если в каждой точке
, если в каждой точке 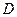 сходится ряд
сходится ряд 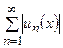 .
.
 2015-04-23
2015-04-23 519
519








