Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: 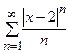 . Применим признак Даламбера:
. Применим признак Даламбера:
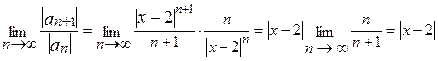 .
.
Если 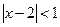 , то ряд сходится. Итак,
, то ряд сходится. Итак, 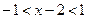 ,
, 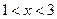 – интервал сходимости данного ряда. Поведение данного ряда на концах интервала сходимости, т.е. в точках
– интервал сходимости данного ряда. Поведение данного ряда на концах интервала сходимости, т.е. в точках 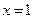 и
и 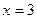 , исследуется отдельно.
, исследуется отдельно.
При 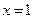 из данного ряда получаем ряд
из данного ряда получаем ряд 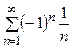 , который условно сходится.
, который условно сходится.
При 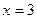 получаем гармонический ряд
получаем гармонический ряд 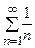 , который расходится.
, который расходится.
Таким образом, данный ряд сходится в области, для которой 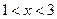 .
.
 2015-04-23
2015-04-23 387
387








