Одной из центральныхзадач в теории степенных рядов является задача разложения элементарных функций в степенные ряды.
Постановка задачи. Пусть дана некоторая функция 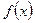 . Требуется установить:
. Требуется установить:
1) может ли эта функция быть представлена на заданном интервале в виде некоторого степенного ряда, т.е. может ли быть «разложена в степенной ряд»?
2) если да, то как найти этот ряд?
Предположим, что для функции 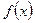 степенной ряд существует, т.е. имеет место разложение.
степенной ряд существует, т.е. имеет место разложение.
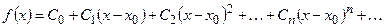
Найдем коэффициенты 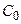 ,
, 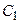 ,
, 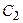 ,...
,...
Если в последнее равенство подставить 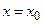 , то получим
, то получим
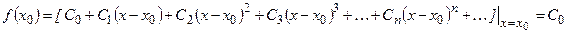
Продифференцируем последовательно обе части равенства и, полагая в полученных равенствах 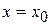 , получим:
, получим:
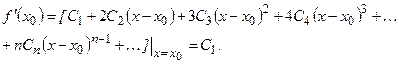
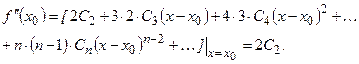
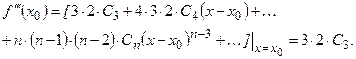
……. ……. …….
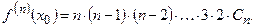
Следовательно, искомые коэффициенты степенного ряда вычисляются по формулам:
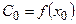 ,
, 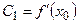 ,
, 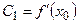 ,
, 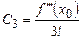 , …,
, …, 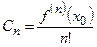 .
.
Подставив найденные коэффициенты, получим
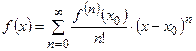 – ряд Тейлора.
– ряд Тейлора.
При 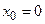 имеем
имеем 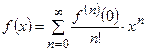 – ряд Маклорена.
– ряд Маклорена.
Ответ на вопрос о возможности разложения функции в степенной ряд дает сформулированная ниже теорема. Предварительно представим 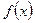 в виде
в виде
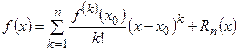 ,
,
где 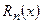 – остаточный член ряда, который может быть представлен в форме Лагранжа
– остаточный член ряда, который может быть представлен в форме Лагранжа 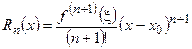 ,
, 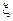 заключено между
заключено между 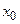 и
и 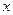 .
.
Теорема. Если функция 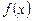 разлагается в степенной ряд по степеням
разлагается в степенной ряд по степеням 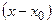 в окрестности точки
в окрестности точки 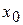 , то этот ряд является рядом Тейлора.
, то этот ряд является рядом Тейлора.
Условия разложимости функции в степенной ряд:
1) 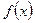 должна иметь в интервале сходимости производные всех порядков.
должна иметь в интервале сходимости производные всех порядков.
2) 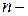 ая частичная сумма ряда Тейлора должна стремиться к
ая частичная сумма ряда Тейлора должна стремиться к 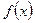 при
при 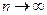 , т.е.
, т.е. 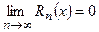 .
.
Условие 2 выполняется, если все производные 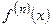 ограничены, т.е. если существует такое число
ограничены, т.е. если существует такое число 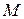 , что во всех точках интервала сходимости
, что во всех точках интервала сходимости 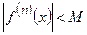 ,
, 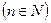 .
.
 2015-04-23
2015-04-23 1794
1794
