Многие практически нужные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, так как первообразная не может быть выражена через конечное число элементарных функций.
Однако, если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости, то можно вычислить определенный интеграл с заданной степенью точности.
Пример 23. Вычислить 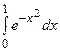 с точностью 0,0001.
с точностью 0,0001.
1) Разложим подынтегральную функцию в ряд:
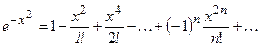 ,
, 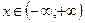 .
.
2) Проинтегрируем его почленно:
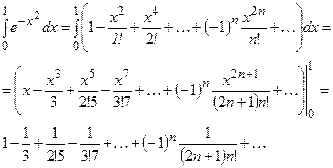
3) Получили знакочередующийся ряд. Для обеспечения требуемой точности достаточно взять сумму первых 7 членов, так как при 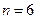

при 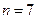
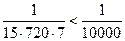 .
.
4) Вычислим приближенно интеграл с одной запасной цифрой.
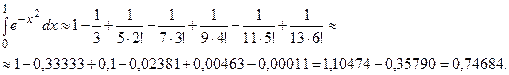
Округляя, получим 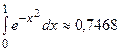 .
.
 2015-04-23
2015-04-23 518
518








