Простейшие разрывные функции

АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ

6.1. Простейшие разрывные функции.

6.2. Физические системы и их математические модели.

6.3. Импульсные и переходные характеристики линейных цепей. Интеграл Дюамеля.

6.4. Частотные характеристики линейных цепей.

6.5. Линейные динамические системы.

6.6. Законы коммутации в линейных цепях.

6.7. Классический метод анализа.

6.8. Спектральный метод анализа.

6.9. Дифференцирующие и интегрирующие цепи.

6.10. Преобразование Лапласа и операторный метод анализа.

Простейшие разрывные функции

Для анализа любых систем и получения их временных характеристик используются две основные разрывные функции.

1. Функция включения. Функция Хэвисайда. Единичный скачок.

Исходной для получения этой функции является функция вида:

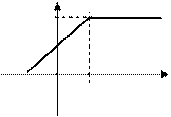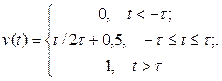
Рассматривая предельный переход при 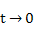, получим функцию включения:

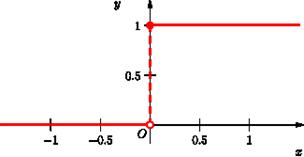
Обозначается как .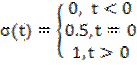

Функция включения используется для описания моментов резкого (или мгновенного) включения или выключения односторонних или ограниченных во времени сигналов, например, прямоугольных импульсов. Она может быть задана относительно любого момента времени, т.е. справедлива при любом временном сдвиге:

.

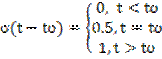2. Дельта – функция.

В качестве исходного для дельта-функции используется импульсный сигнал прямоугольной формы с единичной площадью, который может быть описан при помощи функции включения следующим образом:

;

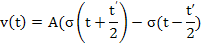при этом: .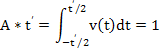

Рассматривая предельный переход при 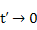, получим 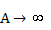и определение дельта-функции:

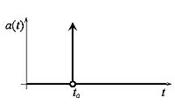
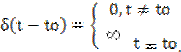
При этом говорят, что дельта-функция сосредоточена в одной точке пространства и ее задание справедливо при любом временном сдвиге.

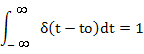
Таким образом, δ-функция представляет собой импульс с бесконечно большой амплитудой, бесконечно малой длительностью и единичной площадью.

Основное свойство δ-функции – «фильтрующее свойство»:

Рассмотрим интеграл от произведения любой произвольной функции f(t) на δ-функцию, сосредоточенную в произвольной точке х по оси времени:

.

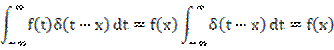Поскольку дельта-функция сосредоточена в одной точке х и равна 0 на всей остальной оси времени, то пределы интегрирования можно свести к малой окрестности этой точки; где любая функция будет иметь свое конкретное постоянное значение f(x), которое можно вынести за знак интеграла. Тогда подынтегральное выражение будет равно 1 в силу условия единичной площади дельта-функции.

Таким образом, δ-функция «отфильтровывает» значение любой функции в той точке, в которой она существует.

Между функцией включения и δ-функцией существует однозначная связь:

.

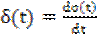Определим спектральную плотность для δ-функции. В силу фильтрующего свойства:

;

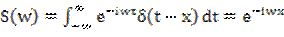где АЧХ (или модуль) всегда равна 1, а ФЧХ (аргумент) определяется положением дельта-функции на оси времени и равен произведению wx.