2015-04-23
2831
Задача анализа – определить законы изменения токов и напряжений на реактивных элементах цепи после коммутации. Поскольку переходный процесс является динамическим процессом, то он описывается соответствующим дифференциальным уравнением вида (6.14). Классический метод анализа основан на классическом же методе решения дифференциальных уравнений, согласно которому полное решение линейного неоднородного (с ненулевой правой частью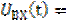 
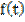¹ 0) дифференциального уравнения n-го порядка с постоянными коэффициентами равно сумме двух решений – установившегося (частного) и свободного(общего):
U = Uy + Ucb. (6.16)
Установившееся решение – это напряжение или ток в новом установившемся режиме после окончания переходного процесса, т.е. при всех нулевых значениях производных: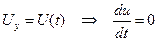 
Свободное решение – это напряжение или ток, которые определяются по формуле:
= 
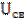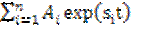(6.17)
где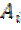 
– постоянные вещественные коэффициенты, определяемые из начальных условий; 
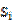- комплексные корни однородного характеристического уравнения n-го порядка 
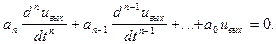Данное уравнение имеет п корней, причем, поскольку коэффициенты вещественны, все корни будут либо вещественными, либо комплексно сопряжёнными.
|
|
|
Рассмотрим на примере последовательной цепи второго порядка алгоритм классического метода анализа:
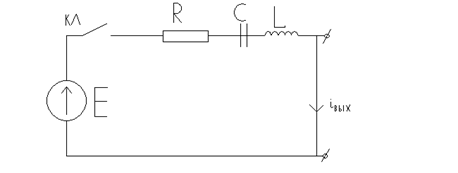
1) Определение начальных условий для электрических величин, которые не изменяются скачком. Для данной схемы такой величиной будет ток, поскольку он является одинаковым для всех элементов и до момента коммутации был равен нулю. Поэтому начальными условиями примем нулевые: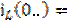 
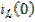= 0.
2) Составление дифференциального уравнения:
.
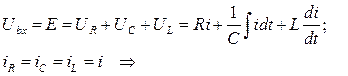
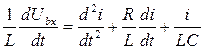Из полученного уравнения можно найти частотный коэффициент передачи (ЧКП), используя (6.15):
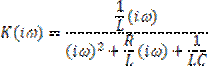
3) Определение установившегося решения при всех нулевых значениях производных:
= 
= 0.
Это говорит об отсутствии тока в цепи после окончания переходного процесса, т.к. в установившемся режиме постоянный ток через зарядившийся конденсатор не проходит (он создает такое же по величине встречное напряжение).
4) Определение свободного решения в соответствии с (6.17):
,
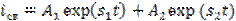где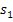 
и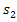 
- корни однородного характеристического уравнения 
,
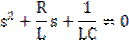причем данное уравнение будет иметь два комплексно-сопряженных корня.
5) Запись полного решения из (6.16): I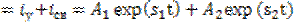 
.
6) Определение коэффициентов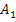 
и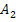 
из начальных условий при t=0:
i(0)= A1 + A2 = 0; → A1 = - A2 = A.
7) Запись решения в окончательном виде: i = A[exp(s1t) – exp(s2t)].
