В структуре любой электронной системы или устройства всегда можно выделить вход, предназначенный для подачи исходных сигналов, и выход, откуда преобразованные сигналы поступают для дальнейшего использования. Обычно это иллюстрируется структурной схемой типа «черного ящика».
В наиболее простом случае как входной сигнал uвх(t), так и выходной сигнал uвых(t), часто называемый откликом или выходной реакцией системы, представляют собой одиночные функции времени. Более общим случаем является представление входного сигнала в виде m-мерного, а выходного – в виде n-мерного векторов:
U вх(t) = {uвх 1(t), uвх 2(t),..., uвх m(t)},
U вых(t) = {uвых 1(t), uвых 2(t),..., uвых n(t)}.
Закон связи между входным и выходным сигналами можно задать посредством системного оператора Т, результатом действия которого на входной сигнал U вх(t) служит выходной U вых(t): U вых(t)=Т U вх(t).
Для полной определенности задачи следует указать также область Dвх некоторого функционального пространства, которая называется областью допустимых входных воздействий. Задание этой области сводится к определению характера входных сигналов (непрерывных или дискретных, детерминированных или случайных). Аналогично должна быть указана область Dвых допустимых выходных сигналов.
Математической моделью физической системы называется совокупность системного оператора Т и двух областей допустимых сигналов Dвх и Dвых. Система называется стационарной, если ее выходная реакция не зависит от того, в какой момент времени поступает входной сигнал, т.е. U вых(t ± t0) = T U вх(t ± t0) и соответствует линейным цепям с постоянными параметрами.
Если же инвариантность свойств системы относительно начала отсчета времени отсутствует, то такая система называется нестационарной (системой с переменными во времени параметрами или параметрической системой) и соответствует линейным цепям с переменными параметрами.
Для линейных систем в силу выполнения принципа суперпозиции справедливы следующие равенства:
Т( U вх 1 + U вх 2) = Т U вх 1 + Т U вх 2;
Т(a U вх) = a Т U вх,
где a - произвольное число.
6.3 Импульсные и переходные характеристики линейных стационарных систем. Интеграл Дюамеля
При динамическом представлении сигналов используют одно из двух элементарных возмущений – единичный скачок (функцию Хэвисайда) или дельта-функцию. Рассмотрим сначала второй принцип, основанный на интегральном представлении сигнала с помощью дельта-функций.
Пусть некоторая стационарная система описывается оператором Т. Будем полагать, что входной и выходной сигналы одномерны. По определению, импульсной характеристикой системы называется функция h(t), являющаяся откликом системы на входной сигнал вида d(t), т.е. h(t) удовлетворяет следующему уравнению:
h(t) = T d(t).
В силу стационарности системы аналогичное уравнение будет справедливо и при смещении входного воздействия во времени на t0:
h(t - t0) = T d(t - t0).
C физической точки зрения импульсная характеристика приближенно отображает реакцию системы на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временем установления стационарного состояния системы.
Интеграл Дюамеля. Знание импульсной характеристики весьма важно, поскольку позволяет формально решить любую задачу о прохождении детерминированного сигнала через такую систему. В силу фильтрующего свойства дельта-функции сигнал всегда может быть представлен следующим образом:
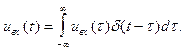
Тогда отвечающая ему выходная реакция:
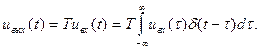 (6.1)
(6.1)
Учитывая, что интеграл есть предельное выражение суммы, то в силу принципа суперпозиции линейный оператор Т может быть внесен под знак интеграла. Далее, оператор Т действует лишь на величины, зависящие от текущего времени t, но не от t. Поэтому (6.1) можно записать в виде:
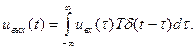
Или, окончательно:
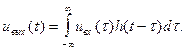 (6.2)
(6.2)
Эта формула, имеющая фундаментальное значение в теории линейных систем, называется интегралом Дюамеля и является основной формулой временного метода анализа систем. Соотношение (6.2) свидетельствует о том, что выходной сигнал линейной стационарной системы представляет собой свертку двух функций – входного сигнала и импульсной характеристики. Очевидно, что (6.2) может быть записано в другом симметричном виде (в силу коммутативности операции свертки):
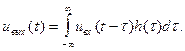
Таким образом, определив импульсную характеристику h(t), дальнейшее решение задачи можно свести к полностью формализованным операциям.
Обобщение на многомерный случай. При изучении более общих случаев, т.е. многомерных систем с m входами и n выходами следует ввести парциальные импульсные характеристики hij(t) (i = 1,2,.., n; j = 1,2,.., m), каждая из которых отображает сигнал на i-ом выходе при подаче на j-ый вход дельта-функции. Совокупность функций hij(t) образует матрицу импульсных характеристик:
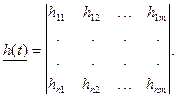
Формула интеграла Дюамеля в многомерном случае приобретает вид:
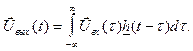 (6.3)
(6.3)
где U вых(t) – n-мерный вектор, U вх(t) – m-мерный вектор.
Условие физической реализуемости. Для любых видов импульсных характеристик физически реализуемых систем всегда должен выполняться важнейший принцип: выходной сигнал, отвечающий импульсному входному воздействию, не может возникнуть до момента подачи сигнала на вход. Изложенный принцип накладывает очень простое ограничение на вид допустимых импульсных характеристик: h(t) = 0 при t < 0.
Для физически реализуемой системы верхний предел в формуле интеграла Дюамеля может быть заменен на текущее значение времени:
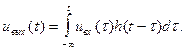 (6.4)
(6.4)
Формула (6.4) имеет ясный физический смысл: линейная стационарная система производит операцию взвешенного суммирования всех мгновенных значений сигнала, поступивших на вход и существовавших «в прошлом» при -¥ < t < t. Роль весовой функции при этом выполняет импульсная характеристика системы. Принципиально важно, что физически реализуемая система ни при каких обстоятельствах не способна оперировать с информацией, заключенной в «будущих» значениях сигнала.
Переходная характеристика. Пусть на входе линейной стационарной системы действует сигнал, изображаемый функцией Хевисайда s(t). Выходную реакцию
g(t) = T s(t) (6.5)
принято называть переходной характеристикой системы. Поскольку рассматриваемая система стационарна, то переходная характеристика инвариантна относительно временного сдвига: g(t - t0) = T s(t - t0).
Принципы физической реализуемости, изложенные для дельта-функции и импульсной характеристики, однозначно должны выполняться и для функции Хевисайда и переходной характеристики. Поэтому последняя отлична от нуля лишь при t ≥ 0, т.е. g(t) = 0 при t<0.
Между импульсной и переходной характеристиками имеется тесная связь. Действительно, поскольку дельта-функция является производной от функции Хевисайда, то на основании определения импульсной характеристики h(t) = T d(t)
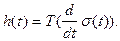
Оператор дифференцирования d/dt и линейный стационарный оператор Т могут меняться местами, и поэтому
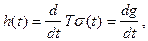 (6.6)
(6.6)
или 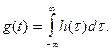 (6.7)
(6.7)
 2015-04-23
2015-04-23 1495
1495
