Группировка данных. Как было указано в п.2.1, множество, полученное в результате наблюдений, представляет собой выборку

Как было указано в п.2.1, множество, полученное в результате наблюдений, представляет собой выборку. Общее количество наблюдений (значений) в выборке называется объемом выборки.

При работе с большим множеством данных приходится их группировать, чтобы получить достаточно наглядную картину колеблемости распределения частот.

В основу группировки закладывается так называемый группировочный признак. Он может быть выражен количественным или качественным значением (например, группировка по видам грузов представляет собой группировку по качественному признаку).

При количественной группировке шкала X разбивается на опреде-ленное число интервалов (групп) и подсчитывается число наблюдений, попавших в данный интервал. Количество значений выборки, попавших в данный интервал, называется частотой группы и обозначается m_i­, где i - номер группы.

Выбор числа интервалов оказывает влияние на получение значений частот. Если после подсчета частот оказалось, что в несколько групп вовсе не попали наблюдения или их попало очень мало, то целе-сообразно уменьшить число интервалов. Обычно берут от 6 до 15 интервалов, но возможны отклонения.

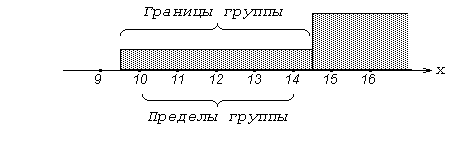
Рис.2.2. Границы и пределы группы для дискретной величины X.

Пределы и границы группы берутся таким образом, чтобы соседние группы не пересекались (см. рис.2.2).

Если наблюдения представляют собой измерения на непрерывной шкале, то обычно берут интервалы с открытым правым концом:

[10-), [15-), и т.д. (2.1)

Среднее группы рассчитывается как среднее арифметическое из пределов: 10+14/2=12.

Рассмотрим пример построения группировочной таблицы.

Пример 2.1. В результате статистического наблюдения за сменной выработкой одного автопогрузчика установлено, что при норме 15 контейнеров фактическая выработка составила:

10 15 13 10 12 22 24 15 12 16

18 20 18 12 16 15 18 20 13 16

15 16 14 13 12 18 14 15 16 15

18 22 18 24 20 13 24 22 18 18

Всего 40 наблюдений показателя (выработки). Обозначим изме-ритель - значение выработки - через Х. Можно подсчитать, сколько раз данное значение X появляется в этой выборке. Например, значение X=13 встречается 4 раза. Следовательно, частота появления этого значения в выборке равна 4.

Пределы дискретных значений показателя в данной выборе: 10 и 24. Поскольку выборка имеет малый объем (n=40), число групп не стоит брать слишком большим, чтобы не дробить картину распределения. В данном случае достаточно разбить весь статистический материал на три группы с пределами: [10-14], [15-19], [20-24]. Группировочная таблица будет выглядеть следующим образом (см. табл.2.3).

Таблица 2.3.

Группировочная таблица для примера 2.1.

Номер груп-пы	Границы группы	Пре- делы группы	Сред-нее группы	Час-тота группы	Относи-тельная частота	Кумуля- тивная частота	Относит. кумулят. частота
i	B	L	`xi	mi	fi	qi	Qi
	9,5-14,5	10-14			0,3		0,3
	14,5-19,5	15-19			0,475		0,775
	19,5-24,5	20-24			0,225		1,000
	Итого:		1,000	-	-

Важным показателем является относительная частота группы, вычис-ляемая по формуле:

m_i

f_i= ¾¾. (2.2)

n

Относительная частота используется для построения специфических диаграмм - частотного многоугольника и гистограммы, позволяющих представить картину колеблемости распределения частот в наглядной графической форме

В предпоследней колонке группировочной таблицы подсчитывается кумулятивная (накопленная) частота, значения которой q_i равны сумме частот i-ой и всех предшествующих групп. Последняя колонка содержит значения относительной кумулятивной частоты, представляющие собой отношения q_i к объему выборки n.