Тема 3.4 Числовые ряды.
Пусть дана бесконечная последовательность чисел 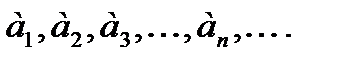
Определение. Выражение 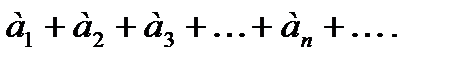 называется бесконечным числовым рядом, или просто рядом.
называется бесконечным числовым рядом, или просто рядом.
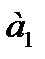 - первый член ряда;
- первый член ряда;
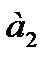 - второй член ряда;
- второй член ряда;
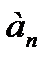 - n -ый или общий член ряда.
- n -ый или общий член ряда.
Коротко ряд можно записать в виде 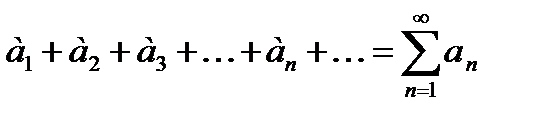 .
.
Здесь:
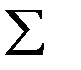 – математический значок суммы;
– математический значок суммы;
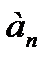 – общий член ряда;
– общий член ряда;
n – переменная-«счётчик».
Запись 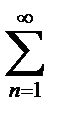 обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала
обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала 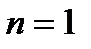 , затем
, затем 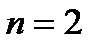 , потом
, потом 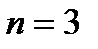 , и так далее – до бесконечности. Вместо переменной n иногда используется переменная k или m. Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля
, и так далее – до бесконечности. Вместо переменной n иногда используется переменная k или m. Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля 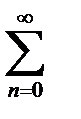 , с двойки
, с двойки 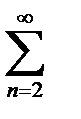 либо с любого натурального числа.
либо с любого натурального числа.
Ряд считается заданным, если известно правило, по которому для любого номера n можно записать соответствующий член ряда, т.е. задан общий член ряда 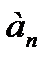 , как функция номера n:
, как функция номера n: 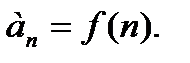
Пример
Записать первые три члена ряда 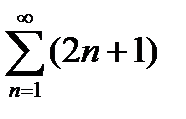 .
.
Решение.
Выбирая первые три номера, найдем члены ряда с этими номерами:
Сначала 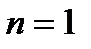 , тогда
, тогда 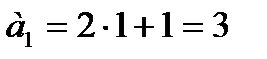 ;
;
Затем 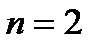 , тогда
, тогда 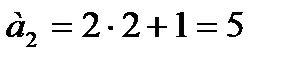 ;
;
Потом 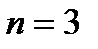 , тогда
, тогда 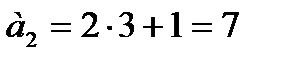 .
.
Процесс можно продолжить до бесконечности, но по условию требовалось написать первые три члена ряда, поэтому ответ: 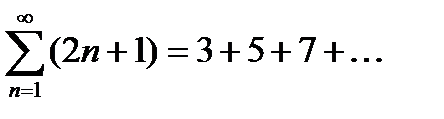
Пример
Записать первые три члена ряда 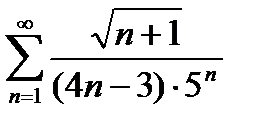 .
.
Решение.
Подставляем в общий член ряда сначала 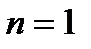 , потом
, потом 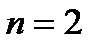 и
и 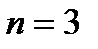 . В итоге:
. В итоге:
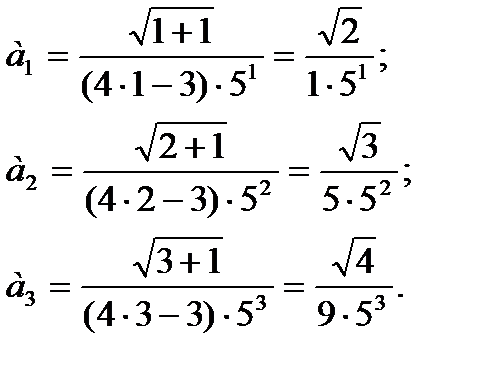
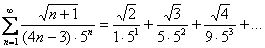
Ответ лучше оставить в таком виде и полученные члены ряда не упрощать, то есть не выполнять действия: 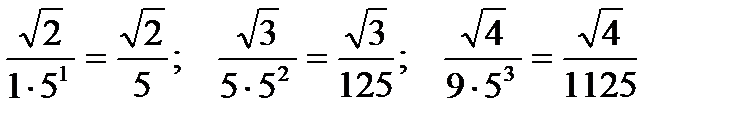 .
.
Иногда встречается обратное задание.
Пример
Записать данный ряд в свёрнутом виде с общим членом ряда: 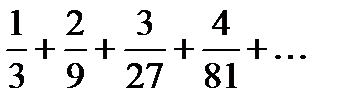
Решение.
Для записи ряда в свернутом виде необходимо найти формулу общего члена ряда. При этом нет какого-то четкого алгоритма решения, закономерность нужно просто увидеть.
В данном случае:
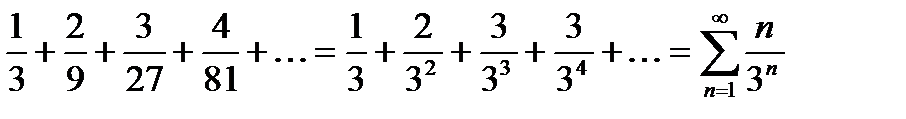
Для проверки полученный ряд 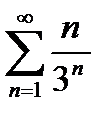 можно «расписать обратно» в развернутом виде.
можно «расписать обратно» в развернутом виде.
Пример
Записать данный ряд в свёрнутом виде с общим членом ряда 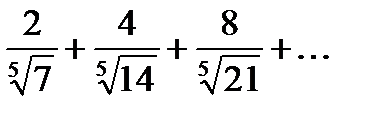
Решение.
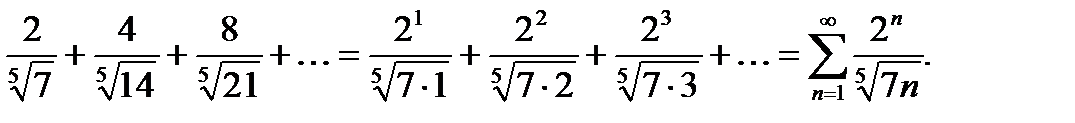
Иногда ряд задается с помощью рекуррентного соотношения, связывающего последующий член ряда с предыдущим. При этом задается несколько первых членов ряда и формула, по которой находятся следующие члены ряда. Например, пусть 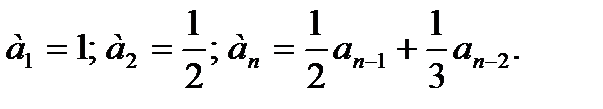
Получим:
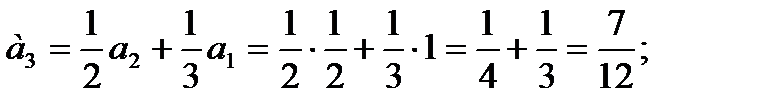
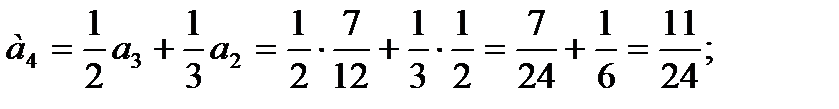 и т.д.
и т.д.
Искомый ряд 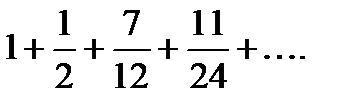
Рассмотрим суммы первых n членов ряда. Такие суммы называют n -ми частичными суммами ряда:
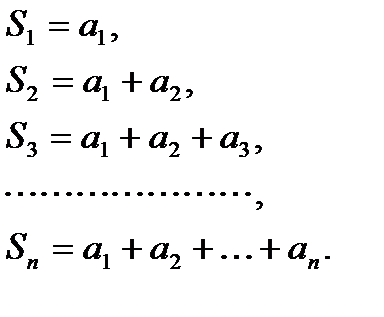
Каждому ряду можно сопоставить последовательность частичных сумм 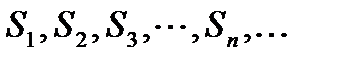 .
.
Одной из ключевых задач теории числовых рядов является исследование ряда на сходимость.
Определение. Ряд называется сходящимся, если существует конечный предел S последовательности его частичных сумм Sn при неограниченном возрастании номера n, т.е. 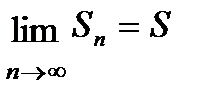 .
.
Предел S последовательности частичных сумм сходящегося ряда называется суммой ряда. Таким образом, если числовой ряд сходится, то его можно просуммировать, т.е. он имеет конечную сумму.
Если последовательность Sn частичных сумм рядане имеет предела или этот предел равен бесконечности, то ряд называется расходящимся.
В качестве примера можно привести бесконечную геометрическую прогрессию:
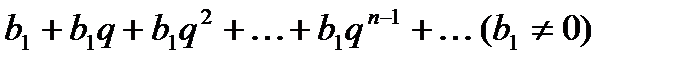 , где q – знаменатель геометрической прогрессии.
, где q – знаменатель геометрической прогрессии.
Для геометрической прогрессии 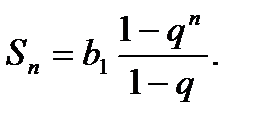
В зависимости от знаменателя, предел суммы членов геометрической прогрессии различен:
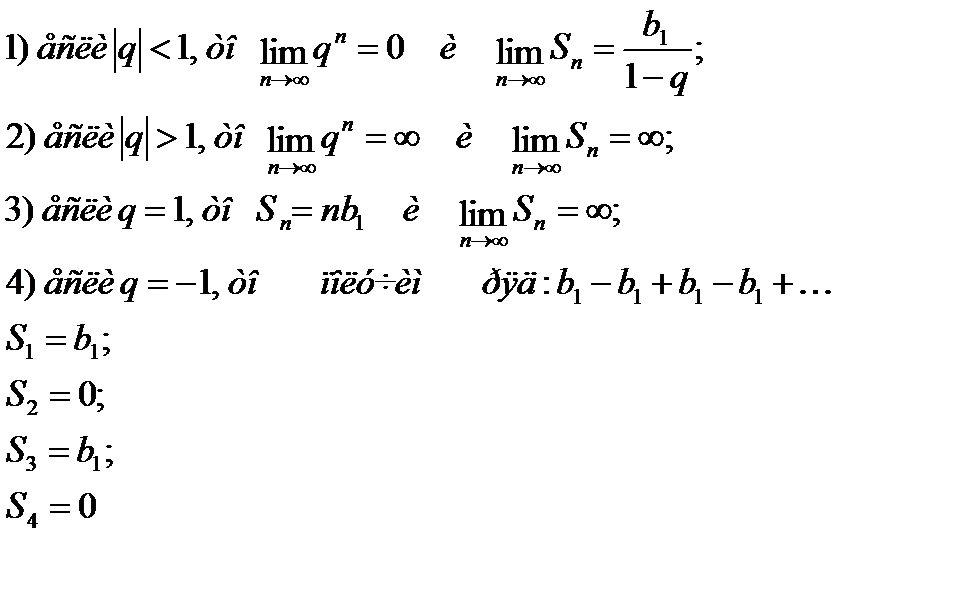
Т.е. Sn не стремится ни к какому пределу.
Окончательно, бесконечная геометрическая прогрессия представляет ряд, который сходится при 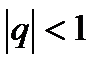 и расходится при
и расходится при 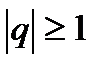 .
.
Ряд вида 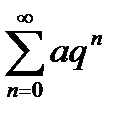 называется геометрическим рядом.
называется геометрическим рядом.
Ряд вида 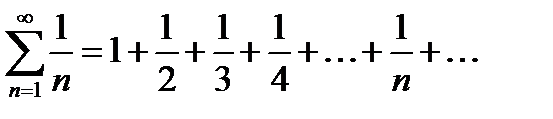 называется гармоническим. Запишем частичную сумму этого ряда, сгруппировав слагаемые следующим образом:
называется гармоническим. Запишем частичную сумму этого ряда, сгруппировав слагаемые следующим образом:
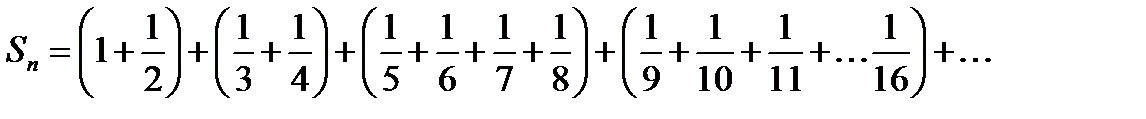
Сумма Sn больше суммы, представленной следующим образом:
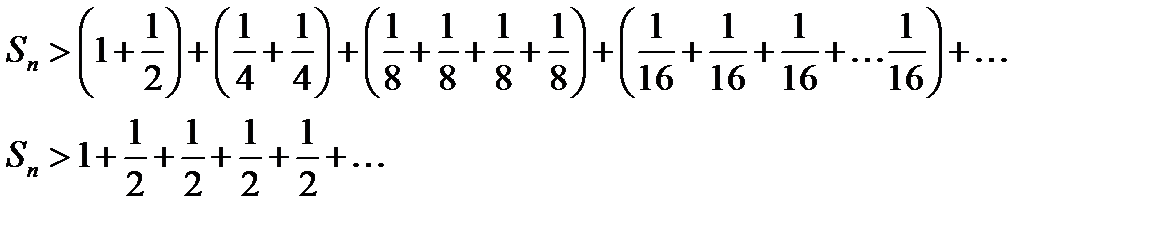
Если 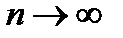 , то
, то 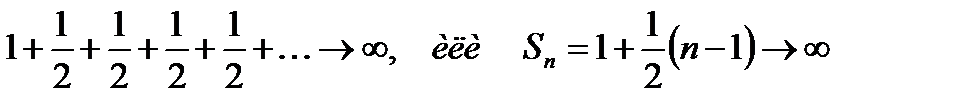 , гармонический ряд расходится.
, гармонический ряд расходится.
Рассмотрим ряд 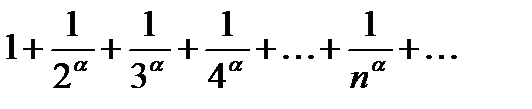 , который называется обобщенным гармоническим рядом.
, который называется обобщенным гармоническим рядом.
1) пусть 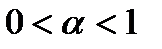
Составим n -ю частичную сумму
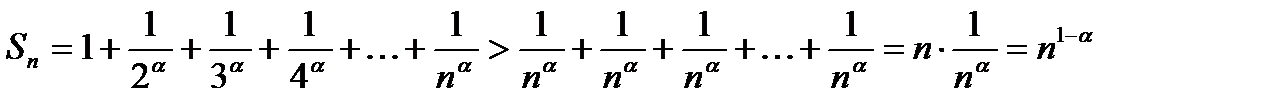
По условию 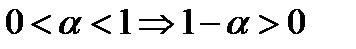 ,
,
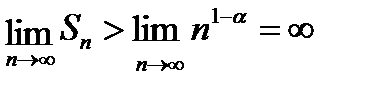 , следовательно, ряд расходится
, следовательно, ряд расходится
2) при 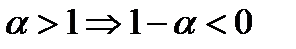 ряд будет сходящимся.
ряд будет сходящимся.
т.о. обобщенный гармонический ряд 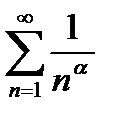 расходится при
расходится при 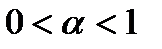 и сходится при
и сходится при 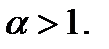
 2015-04-23
2015-04-23 3195
3195







