К методам приближенного и численного интегрирования функций приходится прибегать в случаях, когда
- подынтегральная функция f(x) задана таблично на участке [a,b];
- подынтегральная функция f(x) задана аналитически, но ее первообразная не выражается через элементарные функции;
- подынтегральная функция f(x) задана аналитически, имеет первообразную, но ее определение слишком сложно.
Методы приближенного интегрирования используют разложение подынтегральных функций в ряды Тейлора (Маклорена) и дальнейшего почленного интегрирования членов ряда.
К недостаткам методов приближенного интегрирования относится требование дифференцируемости подынтегральных функций до порядка, который требуется при разложении функций в ряд Тейлора. От этого недостатка свободны методы численного интегрирования, в которых подынтегральная функция удовлетворяет только условию непрерывности (для существования определённого интеграла).
В численных методах интегрирования не используется нахождение первообразной. Основу алгоритма численных методов интегрирования составляет геометрический смысл определенного интеграла. Интеграл численно равен площади S криволинейной трапеции, расположенной под подынтегральной кривой f(x) на участке [a,b]
Суть всех численных методов интегрирования состоит в приближенном вычислении указанной площади. Поэтому все численные методы являются приближенными.
При вычислении интеграла подынтегральная функция f(x) аппроксимируется интерполяционным многочленом
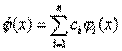 , то есть
, то есть 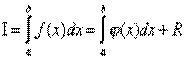 , где
, где 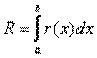 - априорная погрешность метода или остаточный член на интервале интегрирования, а r(x) – априорная погрешность метода на отдельном шаге интегрирования.
- априорная погрешность метода или остаточный член на интервале интегрирования, а r(x) – априорная погрешность метода на отдельном шаге интегрирования.
На практике, чтобы не иметь дело с многочленами высоких степеней, весь участок [a,b] делят на части и интерполяционные многочлены строят для каждой части деления.
Выделяют четыре типа метода численного интегрирования:
1. Методы Ньютона-Котеса. Здесь φ(x) – полином различных степеней. Сюда относятся метод прямоугольников, трапеций, Симпсона.
2. Методы статистических испытаний (методы Монте-Карло). Здесь узлы сетки для квадратурного или кубатурного интегрирования выбираются с помощью датчика случайных чисел, ответ носит вероятностный характер. В основном применяются для вычисления кратных интегралов.
3. Сплайновые методы. Здесь φ(x) – кусочный полином с условиями связи между отдельными полиномами посредством системы коэффициентов.
4. Методы наивысшей алгебраической точности. Обеспечивают оптимальную расстановку узлов сетки интегрирования и выбор весовых коэффициентов ρ(x) в задаче
 Стандартные функции Матлаб:
Стандартные функции Матлаб:




 2015-04-20
2015-04-20 2971
2971
