| Задание 1. Выполнить действия над матрицами: | (А – В)(2 А + Е), где 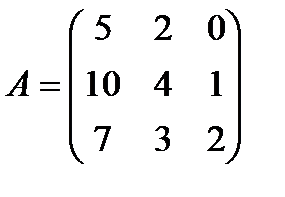 , , 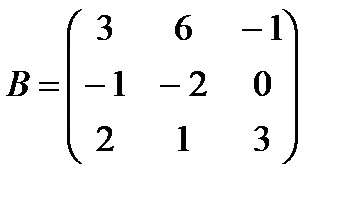 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 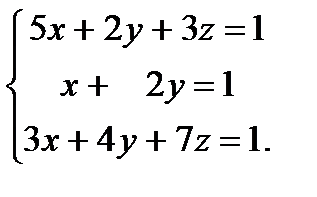 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 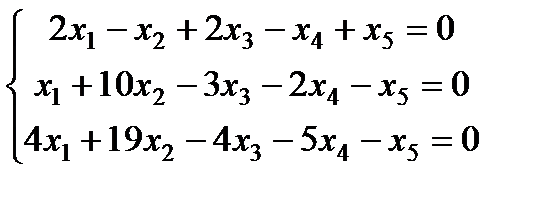 | ||
Задание 4. Даны точки A(1;0;0), B(0;0;2), C(1;0;1), O(0;0;0). Найти угол между векторами 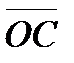 и
и 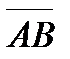 .
.
Задание 5. Вычислить площадь треугольника, вершины которого находятся в точках А(-1;0;-1), В(0;2;-3), С(4;4;1). Найти высоту 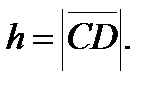
Задание 6. Показать, что точки А(2;-1;-2), В(1;2;1), С(2;3;0), D(5;0;-6) лежат в одной плоскости.
Задание 7. Даны две точки Р(2;3) и Q(–1;0). Составить уравнение прямой, проходящей через точку Q перпендикулярно отрезку PQ.
Задание 8. Написать уравнение плоскости, проходящей через прямые 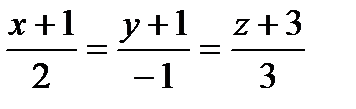 и
и 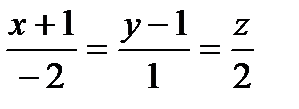 .
.
Задание 9. Написать уравнение окружности, диаметром которой служит отрезок прямой х + у = 6, отсеченный гиперболой ху = 8.
Контрольная работа №2
Задание 1. Даны комплексные числа 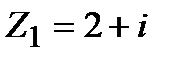 и
и 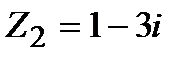 . Найти:
. Найти:
а) 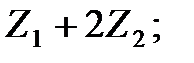 б)
б) 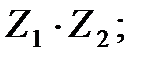 в)
в) 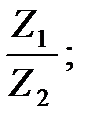 г)
г) 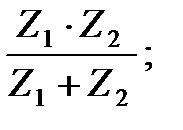 д)
д) 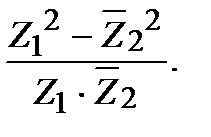
Задание 2. Применяя формулу Муавра, найти 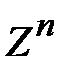 :
: 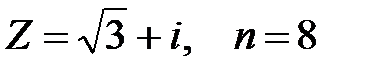 .
.
Задание 3. Найти пределы: а) 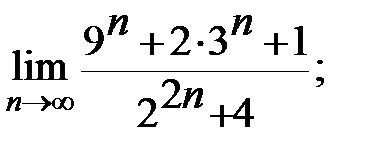 б)
б) 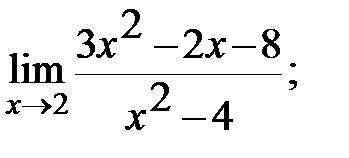
в) 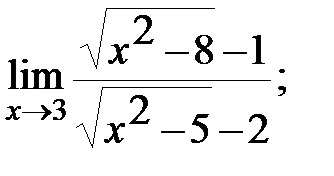 г)
г) 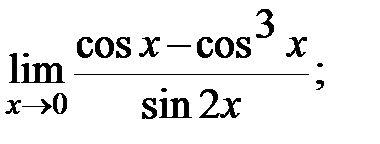 д)
д) 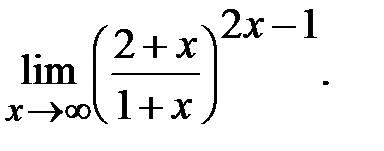
| Задание 4. Найти производные следующих функций: | а) 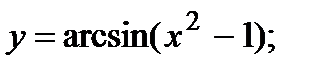 б) б) 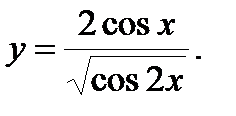 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 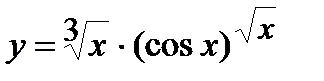 б) б) 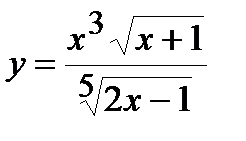 |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | (А – В) А +2 Е, где 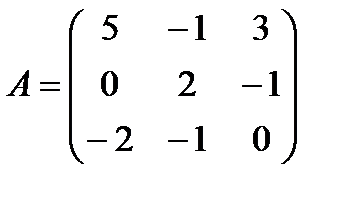 , , 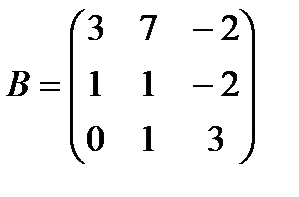 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 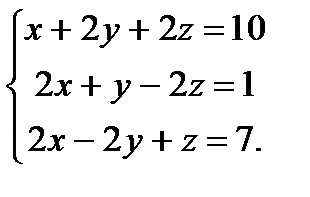 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 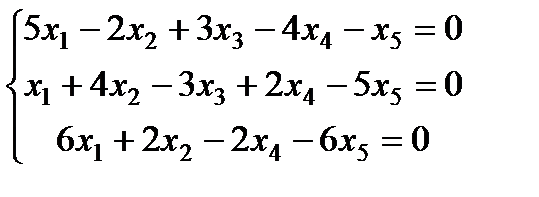 | ||
Задание 4. Найти длину вектора 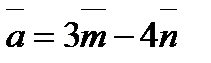 , зная, что
, зная, что 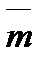 и
и 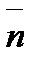 взаимны перпендикулярные орты.
взаимны перпендикулярные орты.
Задание 5. Построить параллелограмм на векторах 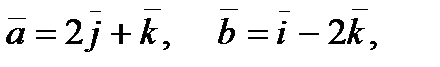 вычислить его площадь и одну из его высот.
вычислить его площадь и одну из его высот.
Задание 6. В тетраэдре с вершинами в точках А(1;1;1), В(2;0;2), С(2;2;2), D(3;4;-3) вычислить высоту 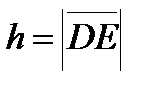 , опущенную на плоскость треугольника АВС.
, опущенную на плоскость треугольника АВС.
Задание 7. Составить уравнение прямой, если точка Р(2;3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.
Задание 8. Найти проекцию точки М 1(3;1;–1) на плоскость 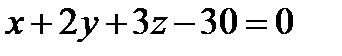 .
.
Задание 9. Определить, как расположена прямая 2х–у–3=0 относительно эллипса 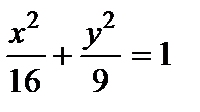 .
.
Контрольная работа №2
Задание 1. Даны комплексные числа 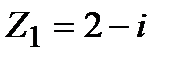 и
и 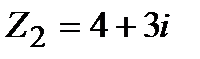 . Найти:
. Найти:
а) 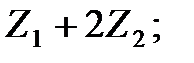 б)
б) 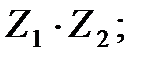 в)
в) 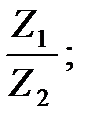 г)
г) 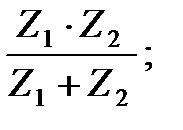 д)
д) 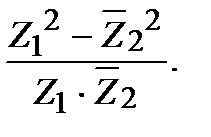
Задание 2. Применяя формулу Муавра, найти 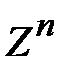 :
: 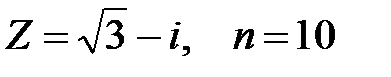 .
.
Задание 3. Найти пределы: а) 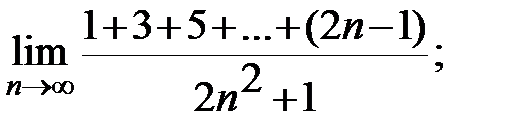 б)
б) 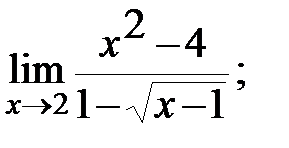
в) 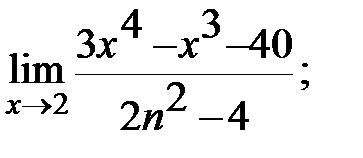 г)
г) 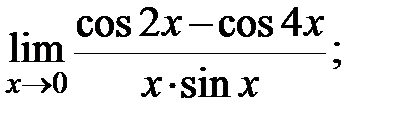 д)
д) 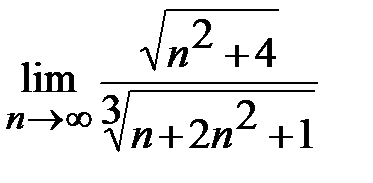
| Задание 4. Найти производные следующих функций: | а) 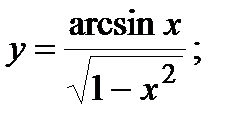 б) б) 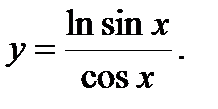 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 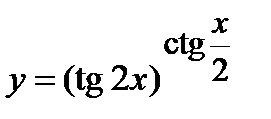 б) б) 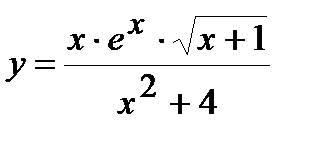 |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | (2 А – В) А + В, где 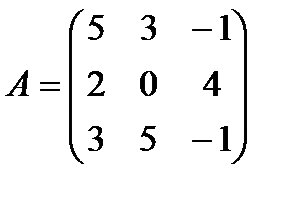 , , 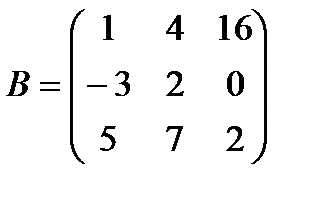 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 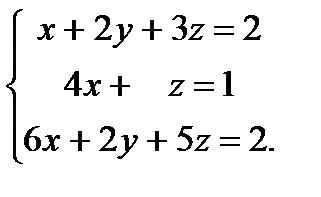 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 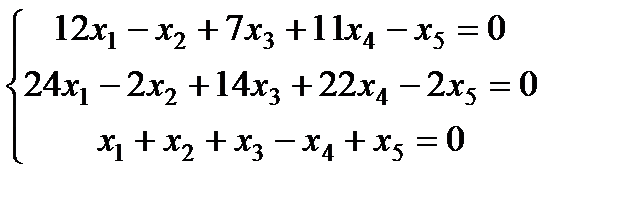 | ||
Задание 4. Векторы 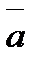 и
и 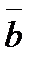 образуют угол
образуют угол 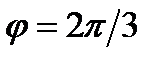 , причем
, причем 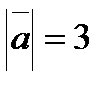 ,
, 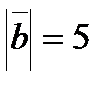 . Определить
. Определить 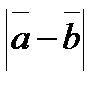 .
.
Задание 5. Вычислить площадь параллелограмма, построенного на векторах 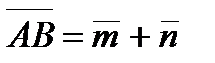 и
и 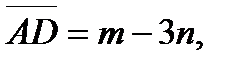 если
если 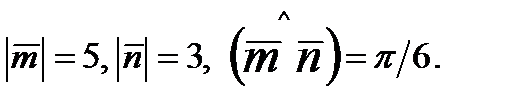
Задание 6. Вычислить объем пирамиды с вершинами в точках О(0;0;0), А(5;2;0), В(2;5;0), С(1;2;4).
Задание 7. Составить уравнение прямой, параллельной двум данным прямым 2 х + 3 у – 6 = 0 и 4 х + 6 у + 17 = 0, проходящей посередине между ними.
Задание 8. Написать уравнение перпендикуляра к плоскости 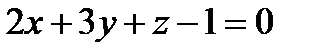 , проходящего через точку пересечения этой плоскости с прямой
, проходящего через точку пересечения этой плоскости с прямой 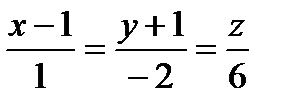 .
.
Задание 9. Составить уравнение окружности, касающейся двух параллельных прямых
2 х + у – 5 = 0, 2 х + у + 15 = 0 и проходящей через точку А (2;1).
Контрольная работа №2
Задание 1. Даны комплексные числа 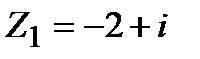 и
и 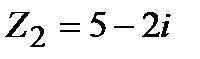 . Найти:
. Найти:
а) 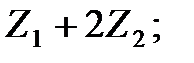 б)
б) 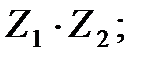 в)
в) 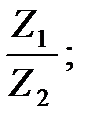 г)
г) 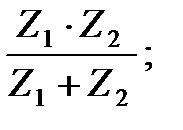 д)
д) 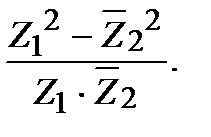
Задание 2. Применяя формулу Муавра, найти 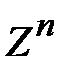 :
: 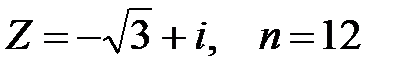 .
.
Задание 3. Найти пределы: а) 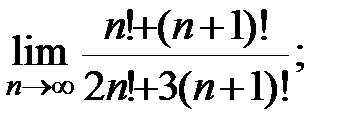 б)
б) 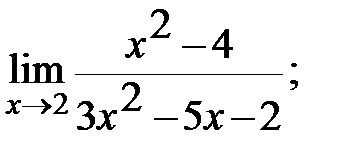 в)
в) 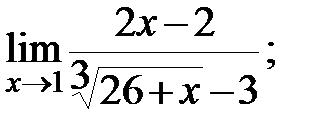
г) 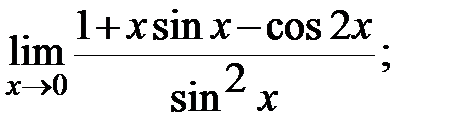 д)
д) 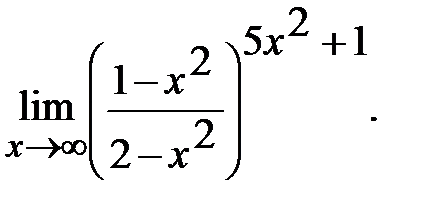
| Задание 4. Найти производные следующих функций: | а) 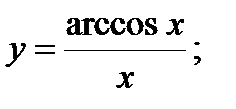 б) б) 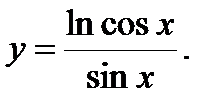 | |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 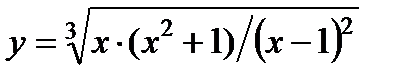 ; б) ; б) 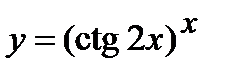 . . | |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | (А – В) А + 3 В, где 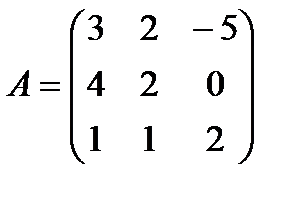 , , 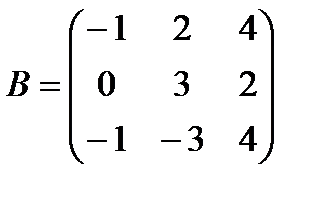 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 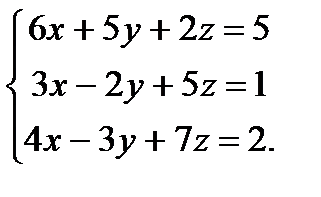 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 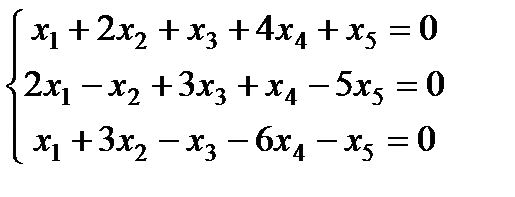 | ||
Задание 4. Даны векторы 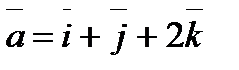 ,
, 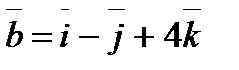 . Определить
. Определить 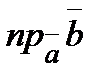
Задание 5. Векторы 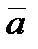 и
и 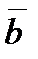 составляют угол 450. Найти площадь треугольника, построенного на векторах
составляют угол 450. Найти площадь треугольника, построенного на векторах 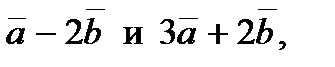 если
если 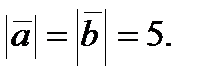
Задание 6. Показать, что векторы 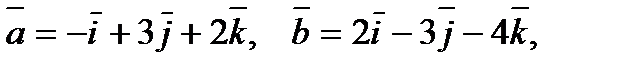
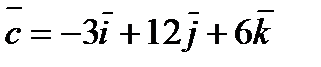 компланарны.
компланарны.
Задание 7. Составить уравнение прямой, проходящей через точку Р(3;5) и на одинаковых расстояниях от точек А(–7;3) и В(11;–15).
Задание 8. Составить уравнение плоскости, проходящее через точку М 0 (1;–1;–1), перпендикулярно к прямой 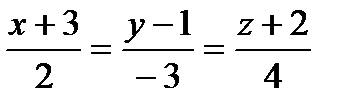 .
.
Задание 9. Привести уравнение кривой к каноническому виду и построить ее:
х 2 + 4 х + 4 у – 2 = 0.
Контрольная работа №2
Задание 1. Даны комплексные числа 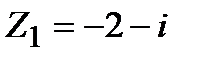 и
и 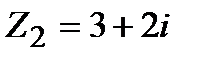 . Найти:
. Найти:
а) 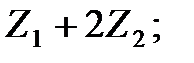 б)
б) 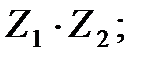 в)
в) 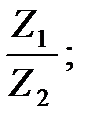 г)
г) 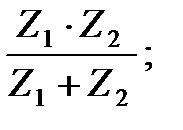 д)
д) 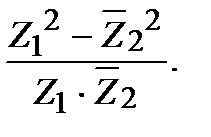
Задание 2. Применяя формулу Муавра, найти 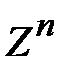 :
: 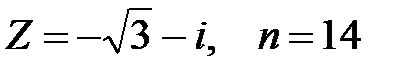 .
.
Задание 3. Найти пределы: а) 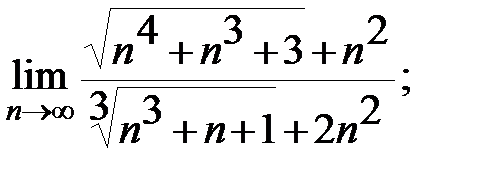 б)
б) 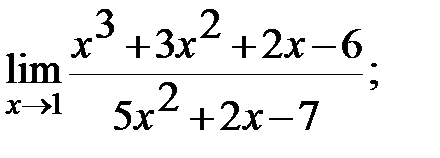
в) 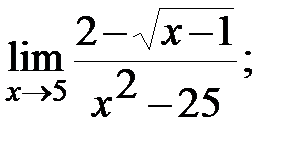 г)
г) 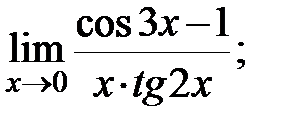 д)
д) 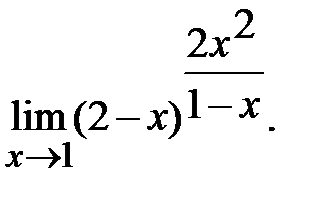
| Задание 4. Найти производные следующих функций: | а) 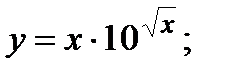 б) б) 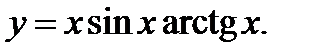 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 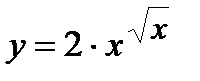 ; б) ; б) 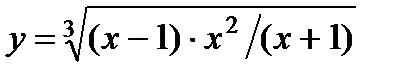 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | 2 А + (А + Е) В, где 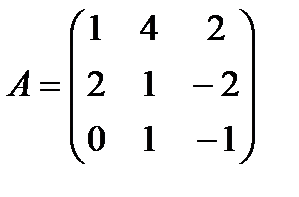 , , 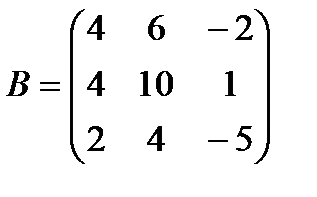 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 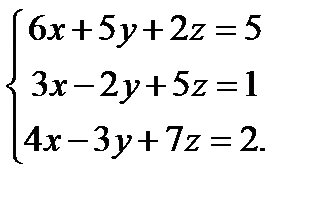 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 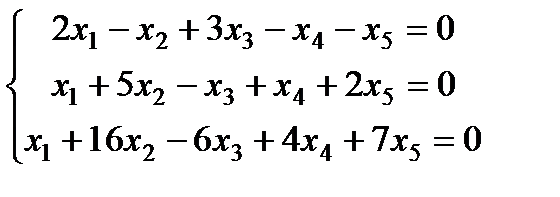 | ||
Задание 4. Даны вершины четырехугольника A(1;-2;2), B(1;4;0), C(-4;1;1), D(-5;-5;3). Доказать, что его диагонали 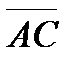 и
и 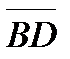 взаимно перпендикулярны
взаимно перпендикулярны
Задание 5. Векторы 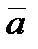 и
и 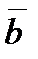 взаимно перпендикулярны. Зная, что
взаимно перпендикулярны. Зная, что 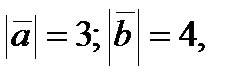 вычислить
вычислить 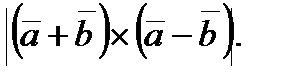
Задание 6. Вектор 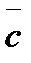 перпендикулярен к векторам
перпендикулярен к векторам 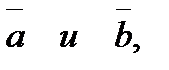 угол между которыми равен
угол между которыми равен 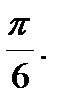 Зная, что
Зная, что 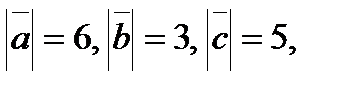 вычислить
вычислить 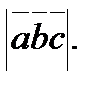
Задание 7. Найти проекцию точки Р(–8;12) на прямую, проходящую через точки А(2;–3) и В(–5;1).
Задание 8. На оси Оz найти точку, расстояние которой от плоскости 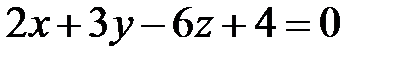 равно 2.
равно 2.
Задание 9. Установить тип кривой, ее характеристики: центр, вершины, фокусы, эксцентриситет, уравнения директрис: 4х2+3у2–8х+12у–32=0. Построить кривую.
Контрольная работа №2
Задание 1. Даны комплексные числа 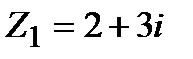 и
и 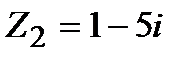 . Найти:
. Найти:
а) 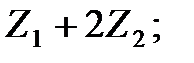 б)
б) 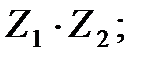 в)
в) 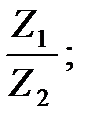 г)
г) 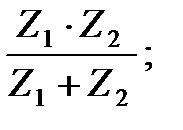 д)
д) 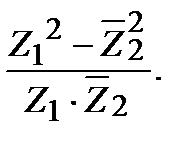
Задание 2. Применяя формулу Муавра, найти 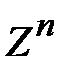 :
: 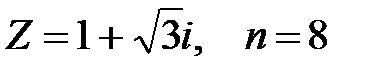 .
.
Задание 3. Найти пределы: а) 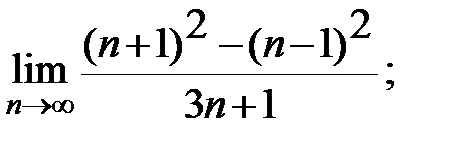 б)
б) 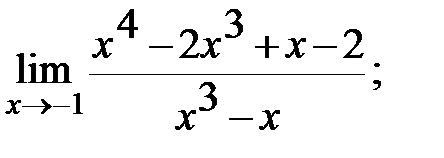
в) 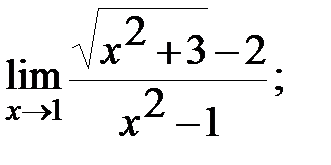 г)
г) 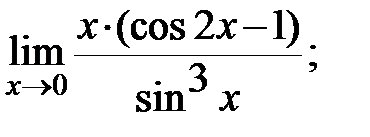 д)
д) 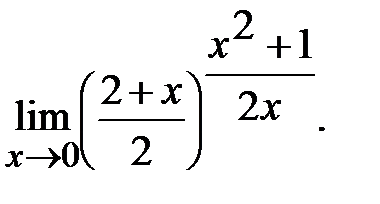
| Задание 4. Найти производные следующих функций: | а) 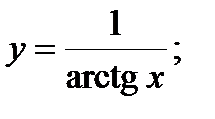 б) б) 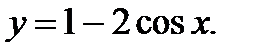 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 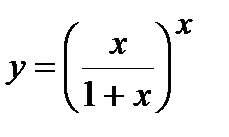 ; б) ; б) 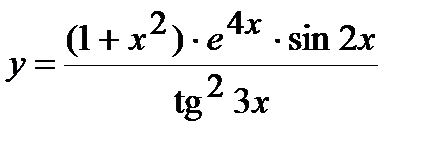 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | 3(А – В) – 2 АВ, где 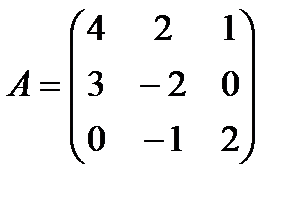 , , 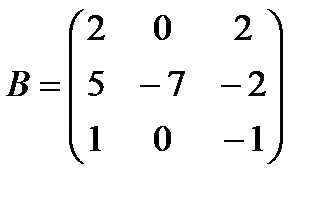 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 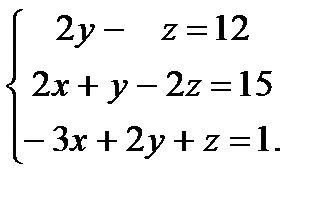 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 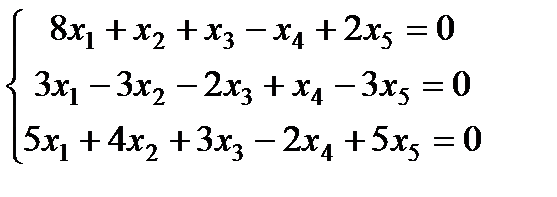 | ||
Задание 4. Даны три вектора 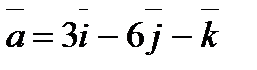 ,
, 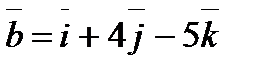 ,
, 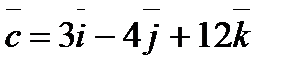 . Вычислить
. Вычислить 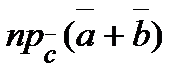
Задание 5. Векторы 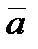 и
и 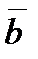 образуют угол
образуют угол 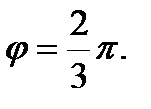 Зная, что
Зная, что 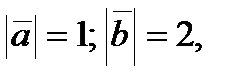 вычислить
вычислить 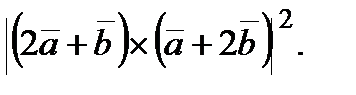
Задание 6. Установить, компланарны ли векторы 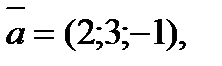
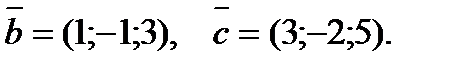
Задание 7. Найти точку М1, симметричную точке М2(8;–9) относительно прямой, проходящей через точки А(3;–4) и В(–1;–2).
Задание 8. Составить уравнение плоскости, проходящей через точку М (1;–2;1) перпендикулярно прямой 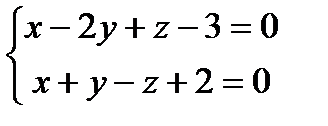 .
.
Задание 9. Определить точки гиперболы 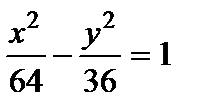 , расстояние которых до правого фокуса равно 4,5.
, расстояние которых до правого фокуса равно 4,5.
Контрольная работа №2
Задание 1. Даны комплексные числа 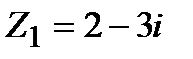 и
и 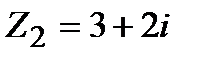 . Найти:
. Найти:
а) 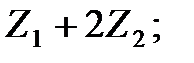 б)
б) 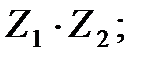 в)
в) 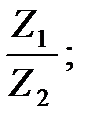 г)
г) 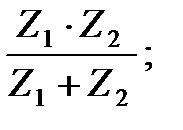 д)
д) 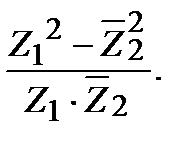
Задание 2. Применяя формулу Муавра, найти 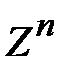 :
: 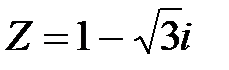 , n =12.
, n =12.
Задание 3. Найти пределы: а) 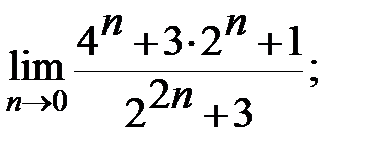 б)
б) 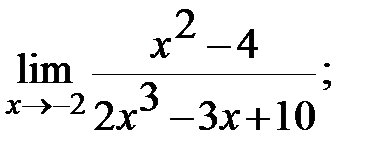
в) 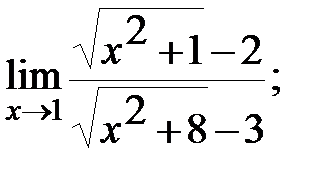 г)
г) 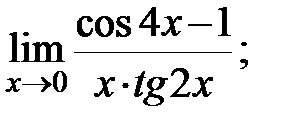 д)
д) 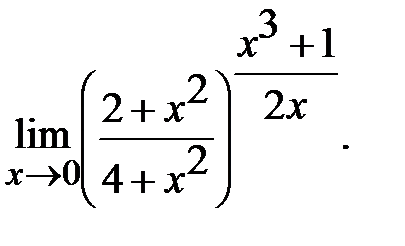
| Задание 4. Найти производные следующих функций: | а) 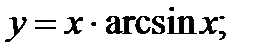 б) б) 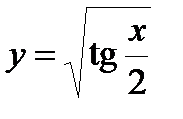 . . |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 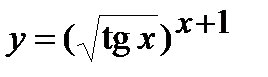 ; б) ; б) 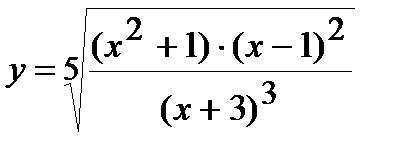 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | (2 А – Е) А + 2 АВ, где 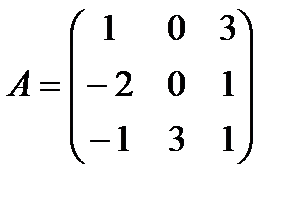 , , 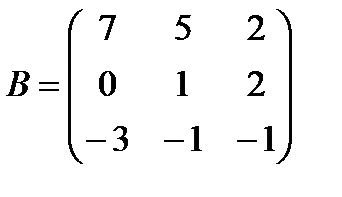 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 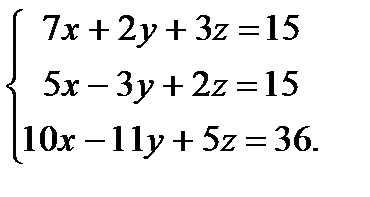 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 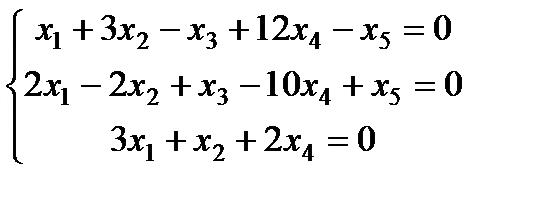 | ||
Задание 4. Даны вершины треугольника A(1;-2;4), B(-4;-2;0), C(3;-2;1). Определить внутренний угол при вершине B.
Задание 5. Даны вершины треугольника А(1;-1;2), В(5;-6;2), С(1;3;-1). Вычислить длину его высоты, опущенной из вершины В на сторону АС.
Задание 6. Доказать, что четыре точки А(1;2;-1), В(0;1;5), С(-1;2;1), D(2;1;3) лежат в одной плоскости.
Задание 7. Вычислить площадь треугольника, отсекаемого прямой 3 х – 4 у – 12 = 0 от координатного угла.
Задание 8. Вычислить объем пирамиды ограниченной плоскостью 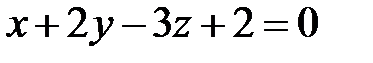 и координатными плоскостями и найти расстояние от начала координат до данной плоскости.
и координатными плоскостями и найти расстояние от начала координат до данной плоскости.
Задание 9. Написать уравнение окружности, проходящей через точку М(1;2) и касающейся осей координат.
Контрольная работа №2
Задание 1. Даны комплексные числа 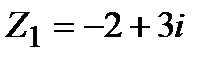 и
и 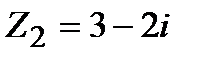 . Найти:
. Найти:
а) 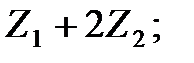 б)
б) 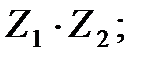 в)
в) 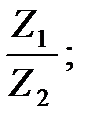 г)
г) 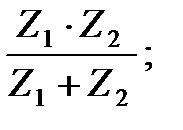 д)
д) 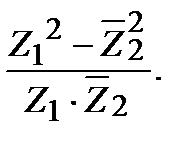
Задание 2. Применяя формулу Муавра, найти 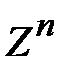 :
: 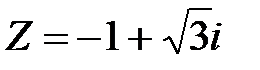 , n = 12.
, n = 12.
Задание 3. Найти пределы: а) 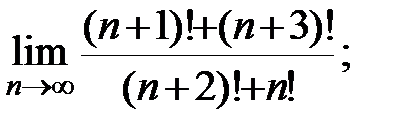 б)
б) 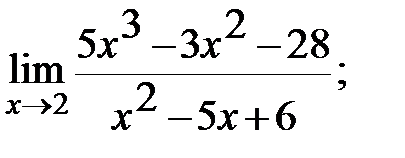
в) 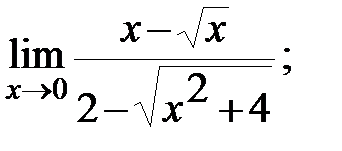 г)
г) 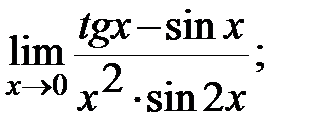 д)
д) 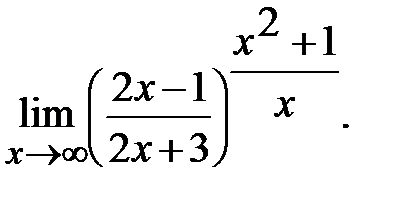
| Задание 4. Найти производные следующих функций: | а) 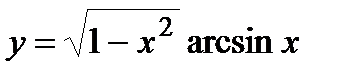 б) б) 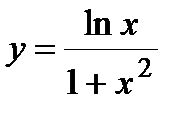 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 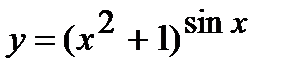 ; б) ; б) 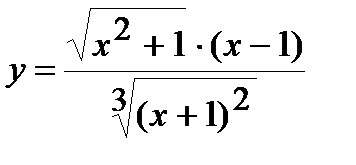 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | А (А – Е) – (А + В) В, где 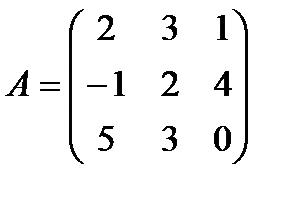 , , 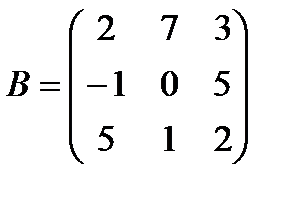 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 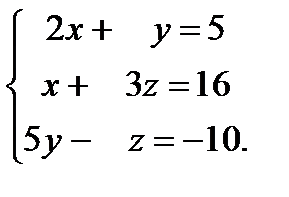 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 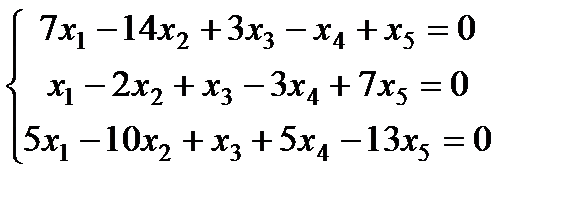 | ||
Задание 4. Вычислив внутренние углы треугольника с вершинами A(1;2;1), B(3;-1;7), C(7;4;-2), доказать, что этот треугольник равнобедренный.
Задание 5. Вычислить синус угла, образованного векторами 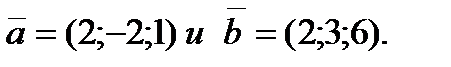
Задание 6. Вычислить объем тетраэдра, вершины которого находятся в точках А(2;-1;1), В(5;5;4), С(3;2;-1), D(4;1;3).
Задание 7. Составить уравнение прямой, которая проходит через точку М1(3;–7) и отсекает на координатных осях отрезки одинаковой величины, отличные от нуля.
Задание 8. Доказать, что прямые 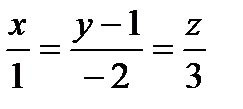 и
и 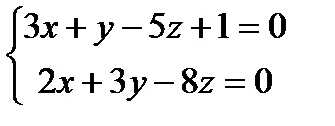 взаимно перпендикулярны.
взаимно перпендикулярны.
Задание 9. Привести уравнение к каноническому виду, найти координаты центра, вершин, фокусов, эксцентриситет, уравнения директрис: 5х2+9у2–30х+18у+9=0. Построить кривую.
Контрольная работа №2
Задание 1. Даны комплексные числа 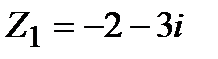 и
и 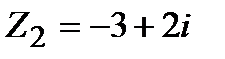 . Найти:
. Найти:
а) 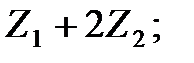 б)
б) 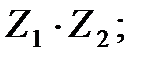 в)
в) 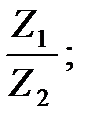 г)
г) 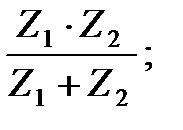 д)
д) 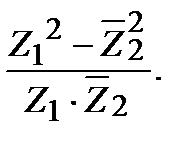
Задание 2. Применяя формулу Муавра, найти 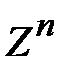 :
: 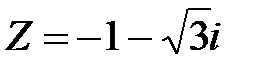 , n = 14.
, n = 14.
Задание 3. Найти пределы: а) 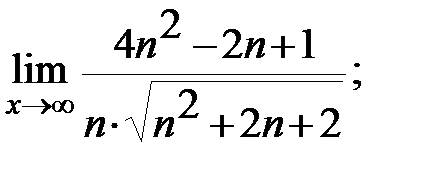 б)
б) 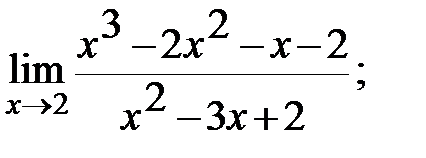
в) 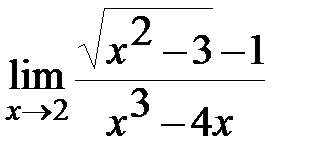 ; г)
; г) 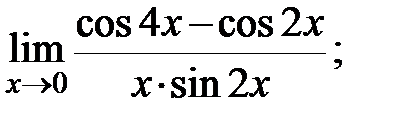 д)
д) 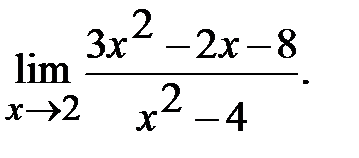
| Задание 4. Найти производные следующих функций: | а) 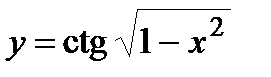 б) б) 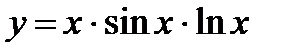 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 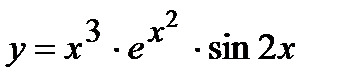 ; б) ; б) 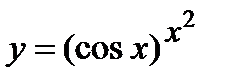 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | (А + В) – В (2 А + Е), где 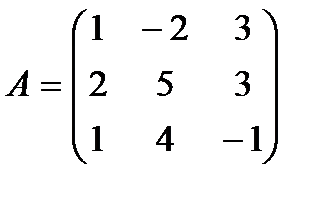 , , 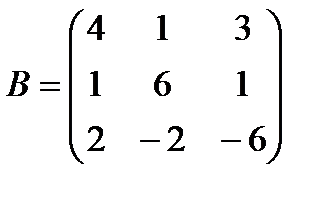 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 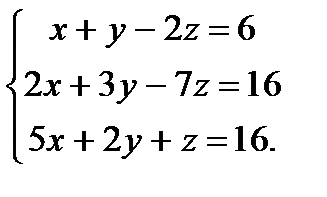 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 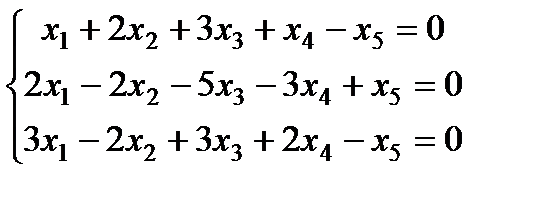 | ||
Задание 4. Векторы 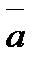 и
и 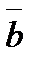 образуют угол
образуют угол 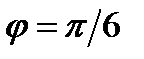 . Зная, что вектор
. Зная, что вектор 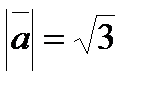 ,
, 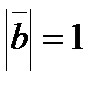 , вычислить угол между векторами
, вычислить угол между векторами 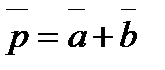 и
и 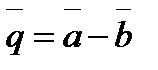 .
.
Задание 5. Векторы 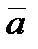 и
и 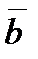 взаимно перпендикулярны. Зная, что
взаимно перпендикулярны. Зная, что 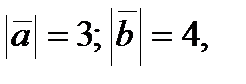 вычислить
вычислить 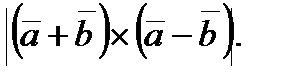
Задание 6. Даны три вершины А(3;-4;7), В(-5;3;-2), С(1;2;-3) параллелограмма АВСD. Найти его четвертую вершину D, противоположную В.
Задание 7. Составить уравнение прямой, которая проходит через точку Р(2;3) и отсекает на координатных осях отрезки равной длины, отличные от нуля.
Задание 8. Составить уравнение плоскости, проходящей через точку А (0;2;1) и параллельной векторам 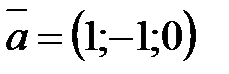 и
и 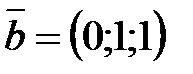 .
.
Задание 9. Привести уравнение к каноническому виду, найти координаты центра, вершин, фокусов, эксцентриситет, уравнения директрис и асимптот: 6 х 2 – 9 у 2 – 64 х – 54 у – 161 = 0. Построить кривую.
Контрольная работа №2
Задание 1. Даны комплексные числа 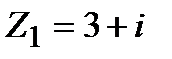 и
и 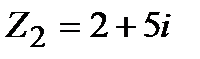 . Найти:
. Найти:
а) 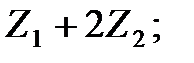 б)
б) 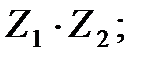 в)
в) 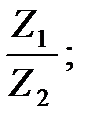 г)
г) 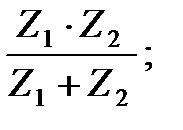 д)
д) 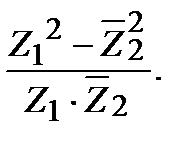
Задание 2. Применяя формулу Муавра, найти 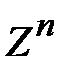 : Z = 3 + 3 i, n = 16.
: Z = 3 + 3 i, n = 16.
Задание 3. Найти пределы: а) 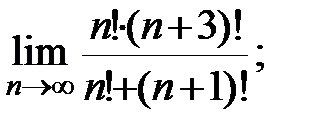 б)
б) 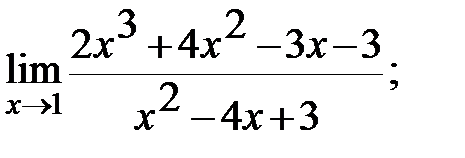
в) 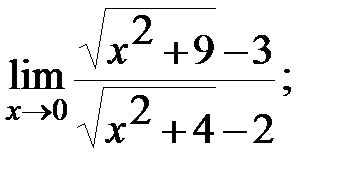 г)
г) 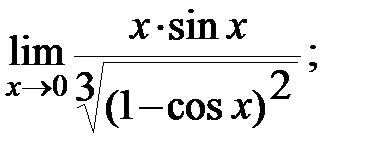 д)
д) 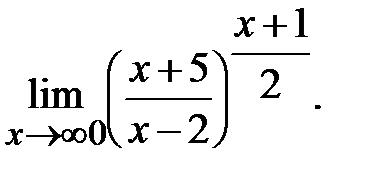
| Задание 4. Найти производные следующих функций: | а) 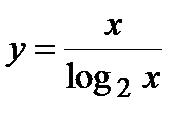 б) б) 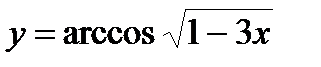 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 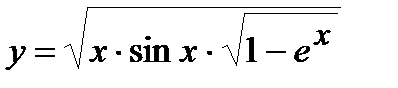 ; б) ; б) 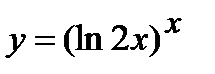 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | А (2 Е + В) – В (А – Е), где 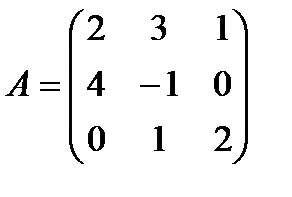 , , 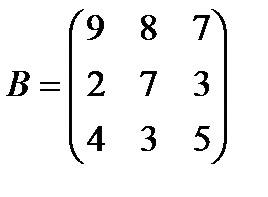 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 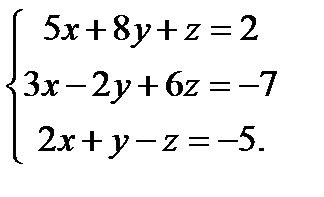 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 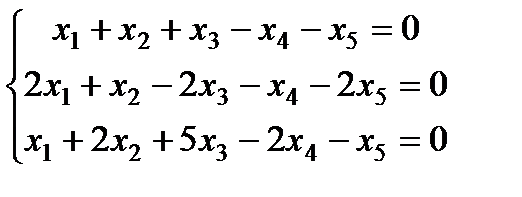 | ||
Задание 4. Даны две точки M(-5;7;-6), N(7;-9;9). Вычислить проекцию вектора 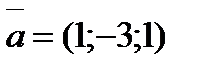 на ось, совпадающую с направлением вектора
на ось, совпадающую с направлением вектора 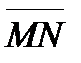 .
.
Задание 5. Вычислить площадь параллелограмма, построенного на векторах 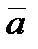 и
и 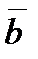 , если известны его диагонали
, если известны его диагонали 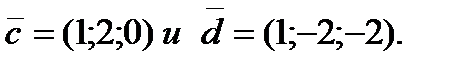
Задание 6. Даны вершины тетраэдра А(2;3;1), В(4;1;-2), С(6;3;7), D(-5;-4;8). Найти длину его высоты, опущенной из вершины D.
Задание 7. Составить уравнение прямой, которая проходит через точку С(8;6) и отсекает от координатного угла треугольник площадью 12 кв.ед.
Задание 8. Найти расстояние от точки М (2;–1;3) до прямой 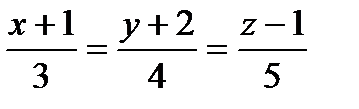 .
.
Задание 9. Написать уравнение параболы, если известны фокус F (4;3) и уравнение директрисы у + 1 = 0.
Контрольная работа №2
Задание 1. Даны комплексные числа 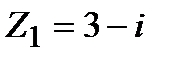 и
и 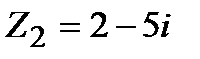 . Найти:
. Найти:
а) 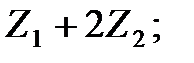 б)
б) 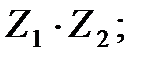 в)
в) 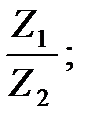 г)
г) 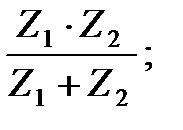 д)
д) 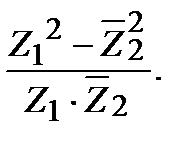
Задание 2. Применяя формулу Муавра, найти 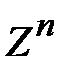 : Z = 3 – 3 i, n = 8.
: Z = 3 – 3 i, n = 8.
Задание 3. Найти пределы: а) 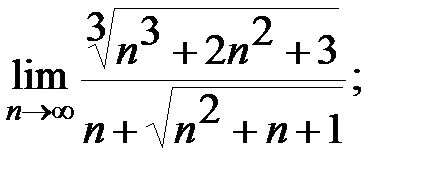 б)
б) 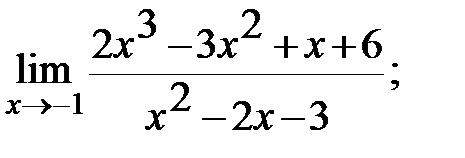
в) 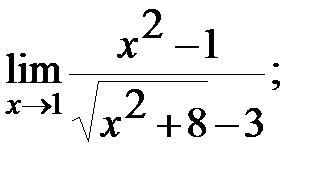 г)
г) 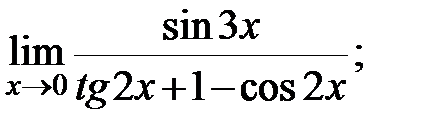 д)
д) 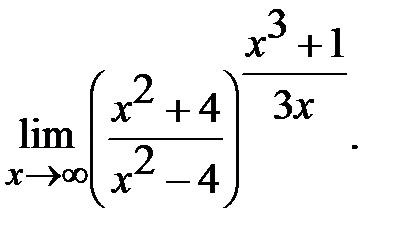
| Задание 4. Найти производные следующих функций: | а) 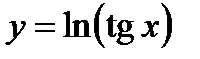 б) б) 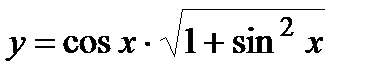 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 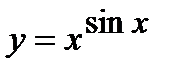 ; б) ; б) 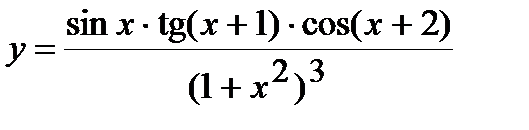 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | 3(А + В)(В – Е), где 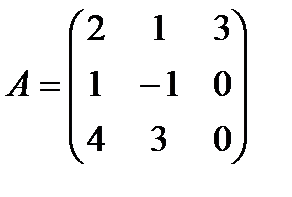 , , 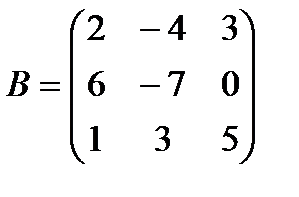 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 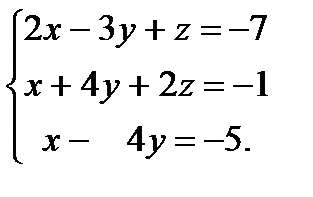 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 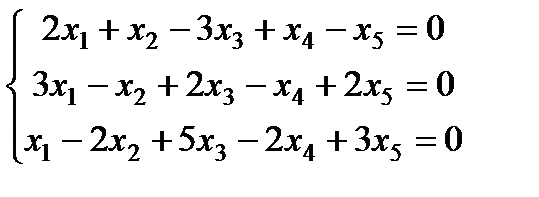 | ||
Задание 4. Векторы 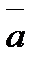 и
и 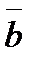 образуют угол
образуют угол 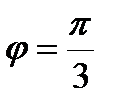 . Зная, что
. Зная, что 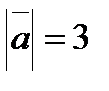 ,
, 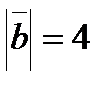 , вычислить
, вычислить 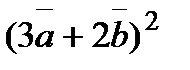 .
.
Задание 5. Даны векторы 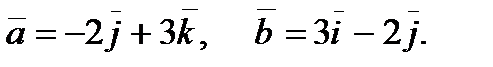 Вычислить площадь треугольника, построенного на этих векторах.
Вычислить площадь треугольника, построенного на этих векторах.
Задание 6. Известны точки А(-1;0;-1), В(1;0;0), С(-2;3;1), D(-1;-2;0). Доказать, что треугольник АВС прямоугольный, а точка D не лежит в плоскости треугольника ABC.
Задание 7. В треугольнике с вершинами А(–2;0), В(2;6) и С(4;2) проведена высота ВD. Написать уравнение этой высоты.
Задание 8. Составить уравнение плоскости, проходящей через точку А (2;–1;3) и отсекающей на осях координат равные отрезки и написать уравнение перпендикуляра к этой плоскости, проходящего через точку А.
Задание 9. Найти угол между радиусами окружности х 2 + у 2 – 4 х + 6 у – 5 = 0, проведенными в точках пересечения ее с осью Ох.
Контрольная работа №2
Задание 1. Даны комплексные числа 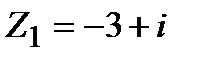 и
и 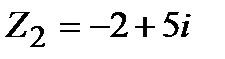 . Найти:
. Найти:
а) 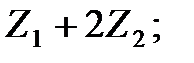 б)
б) 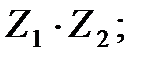 в)
в) 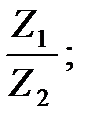 г)
г) 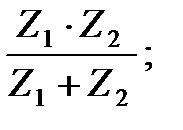 д)
д) 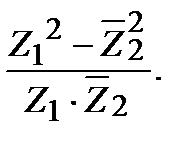
Задание 2. Применяя формулу Муавра, найти 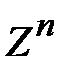 : Z = 3 + 3 i, n = 10.
: Z = 3 + 3 i, n = 10.
Задание 3. Найти пределы: а) 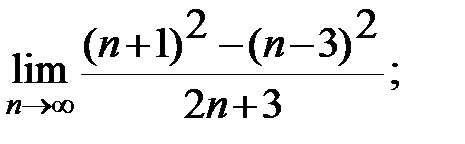 б)
б) 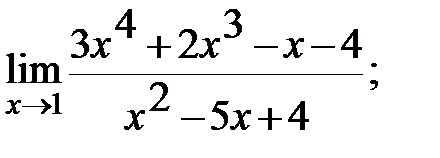
в) 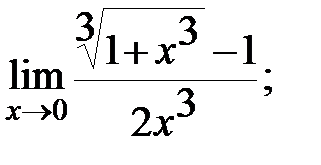 г)
г) 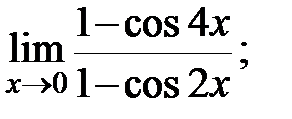 д)
д) 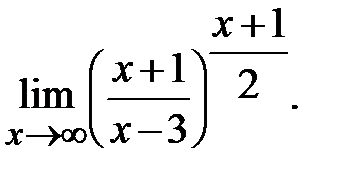
| Задание 4. Найти производные следующих функций: | а) 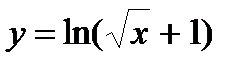 б) б) 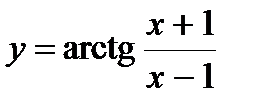 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 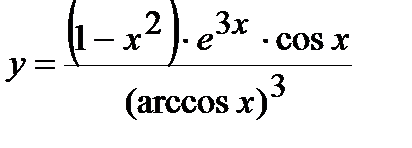 ; б) ; б) 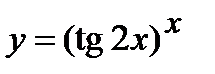 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | (А + В)(2 Е – А), где 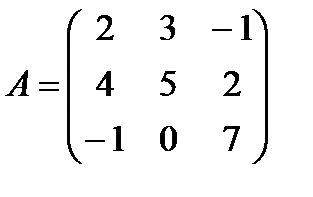 , , 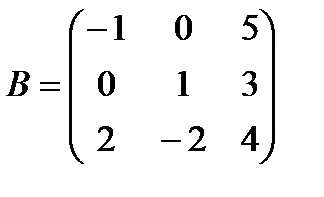 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 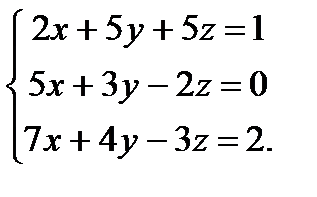 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему реше- ний: | 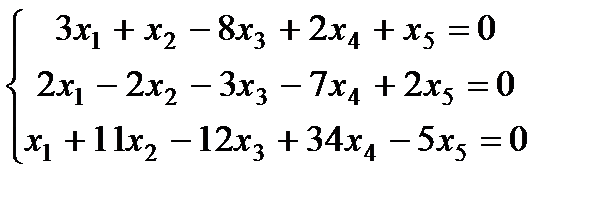 | ||
Задание 4. Даны точки A(3;3;-2), B(0;-3;4), C(0;-3;0), D(0;2;-4). Найти 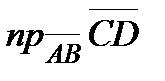
Задание 5. Задан треугольник с вершинами А(1;-2;8), В(0;0;4), С(6;2;0). Вычислить его площадь
и высоту 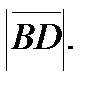
Задание 6. Вычислить объем тетраэдра ОАВС, если 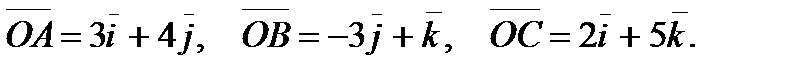
Задание 7. Написать уравнение прямой, проходящей через точку пересечения прямых
2 х –3 у –1 = 0 и 3 х + у – 7 = 0 перпендикулярно к прямой у = 2 х + 5.
Задание 8. Две грани куба лежат на плоскостях 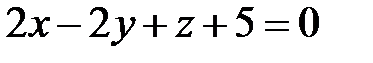 ,
, 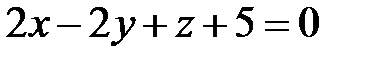 .
.
Вычислить объем этого куба.
Задание 9. Найти расстояние от центра окружности х 2 + у 2 + 2 у =0 до прямой
у = 2 (2 – х).
Контрольная работа №2
Задание 1. Даны комплексные числа 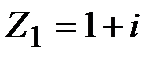 и
и 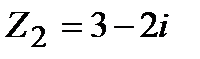 . Найти:
. Найти:
а) 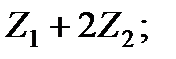 б)
б) 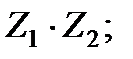 в)
в) 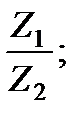 г)
г) 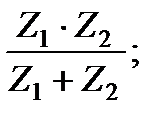 д)
д) 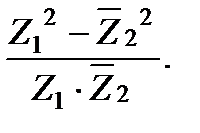
Задание 2. Применяя формулу Муавра, найти 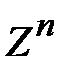 : Z = 1 + i, n=10.
: Z = 1 + i, n=10.
Задание 3. Найти пределы: а) 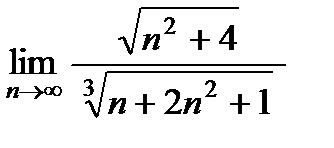 ; б)
; б) 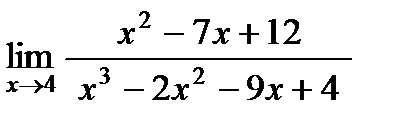 ;
;
в) 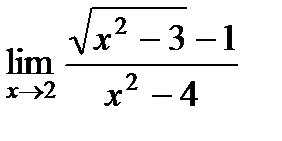 ; г)
; г) 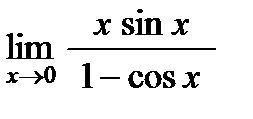 ; д)
; д) 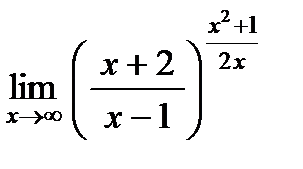 .
.
| Задание 4. Найти производные следующих функций: | а) 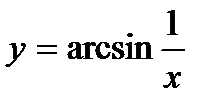 ; б) ; б) 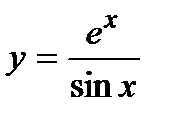 . . |
| Задание 5. Используя формулу логарифмического диф- ференцирования, найти производные следующих функций: | а) 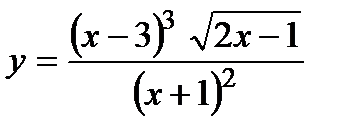 ; б) ; б) 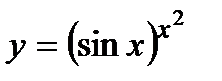 . . |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | А – (Е + 2 В) В, где 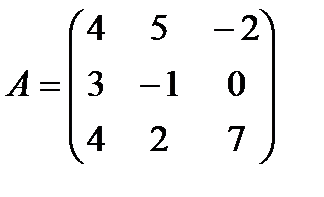 , , 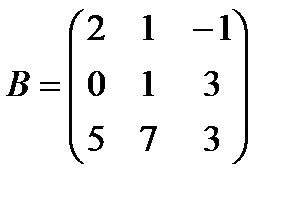 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 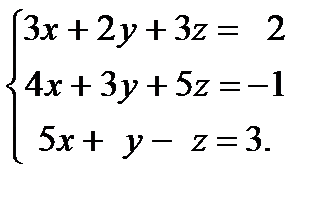 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему реше- ний: | 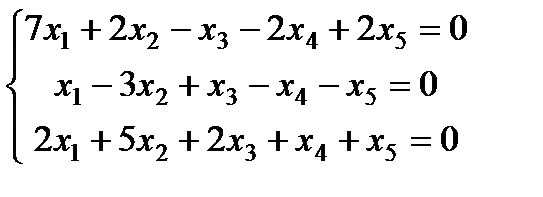 | ||
Задание 4. Вектор 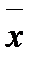 перпендикулярен векторам
перпендикулярен векторам 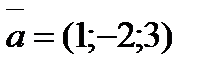 и
и 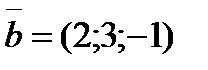 и удовлетворяет усло- вию
и удовлетворяет усло- вию 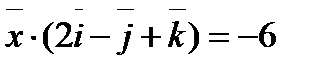 . Найти координаты вектора
. Найти координаты вектора 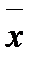 .
.
Задание 5. Даны векторы 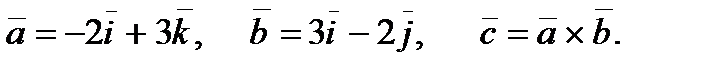 Вычислить модуль вектора
Вычислить модуль вектора 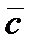 и площадь треугольника, построенного на векторах
и площадь треугольника, построенного на векторах 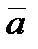 и
и 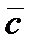 .
.
Задание 6. Вычислить объем тетраэдра с вершинами в точках А(2;-3;5), В(0;2;1), С(-2;-2;-3), D(3;2;4).
Задание 7. Даны уравнения двух сторон прямоугольника 2х–3у+5=0, 3х + 2у – 7 =0 и одна из его вершин А (2;–3). Составить уравнения двух сторон этого прямоугольника.
Задание 8. Показать, что прямая 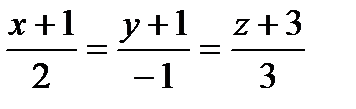 лежит в плоскости
лежит в плоскости 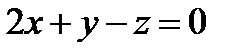 .
.
Задание 9. Определить, как расположена прямая 2х–у–3=0 относительно окружности х2+у2–3х+2у–3=0.
Контрольная работа №2
Задание 1. Даны комплексные числа 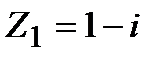 и
и 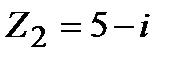 . Найти:
. Найти:
а) 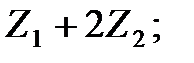 б)
б) 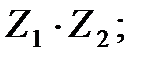 в)
в) 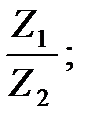 г)
г) 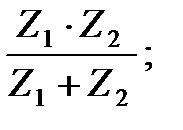 д)
д) 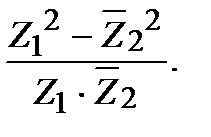
Задание 2. Применяя формулу Муавра, найти 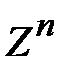 : Z = 1 – i, n = 10.
: Z = 1 – i, n = 10.
Задание 3. Найти пределы: а) 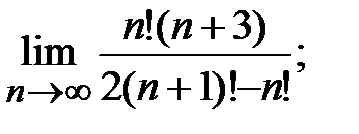 б)
б) 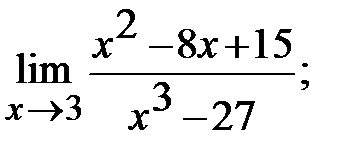
в) 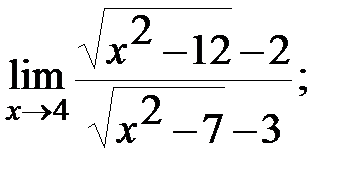 г)
г) 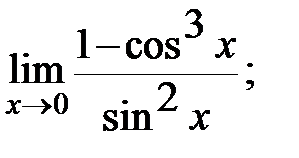 д)
д) 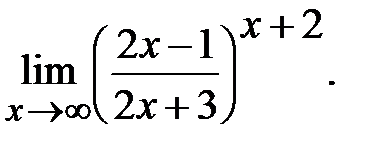
| Задание 4. Найти производные следующих функций: | а) 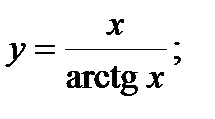 б) б) 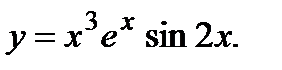 |
| Задание 5. Используя формулу логарифмического диф ференцирования, найти производные следующих функций: | а) 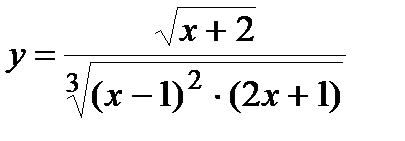 б) б) 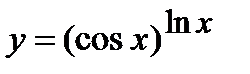 |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | (А – В)(А + В), где 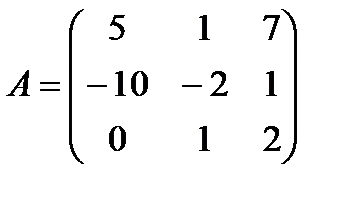 , , 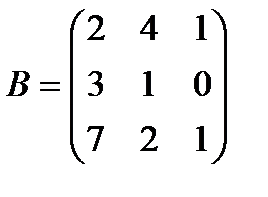 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 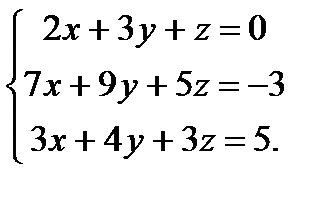 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 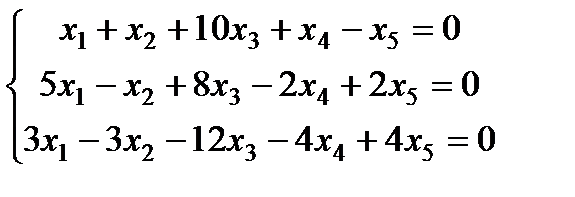 | ||
Задание 4. Доказать, что четырехугольник с вершинами A(–3; 5; 6), B(1; –5; 7), C(8; –3; –3), D(4; 7; –2) является квадратом.
Задание 5. Вычислить диагонали и площадь параллелограмма, построенного на векторах 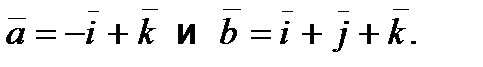
Задание 6. Доказать, что векторы 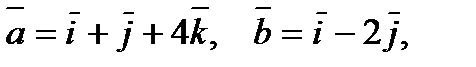
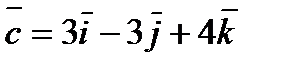 компланарны.
компланарны.
Задание 7. Даны уравнения двух сторон прямоугольника х – 2у = 0, х–2у+15=0 и уравнение одной из его диагоналей 7х+у–15=0. Найти вершины прямоугольника.
Задание 8. Написать уравнение плоскости, проходящей через прямую 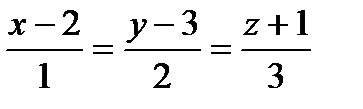 и точку М 0 (3;4;0).
и точку М 0 (3;4;0).
Задание 9. Привести уравнение к каноническому виду и построить кривую х2+4х–5у+19=0.
Контрольная работа №2
Задание 1. Даны комплексные числа 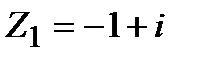 и
и  . Найти:
. Найти:
а) 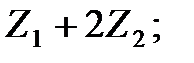 б)
б) 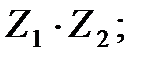 в)
в) 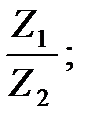 г)
г) 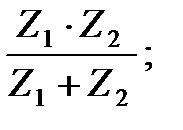 д)
д) 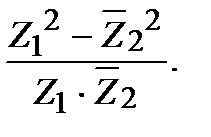
Задание 2. Применяя формулу Муавра, найти 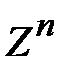 : Z = –1 + i, n = 14.
: Z = –1 + i, n = 14.
Задание 3. Найти пределы: а) 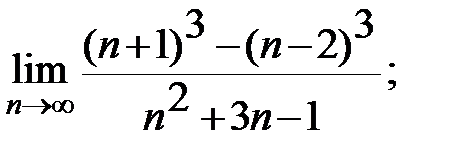 б)
б) 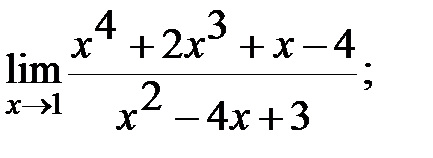
в) 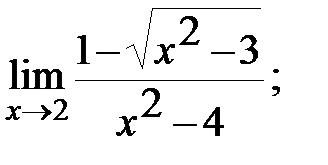 г)
г) 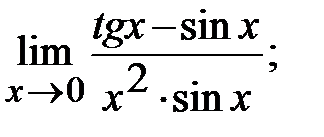 д)
д) 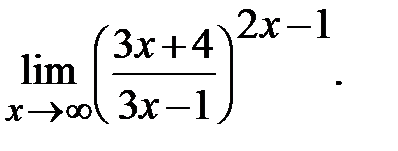
| Задание 4. Найти производные следующих функций: | а) 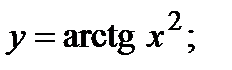 б) б) 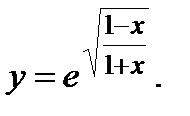 |
| Задание 5. Используя формулу логарифмического дифференцирования, найти производные следующих функций: | а) 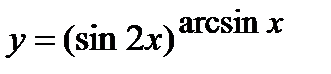 б) б) 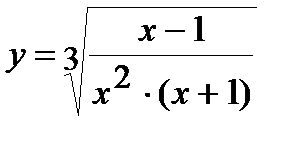 |
Контрольная работа №1
| Задание 1. Выполнить действия над матрицами: | (А – В)(А + 2 В), где 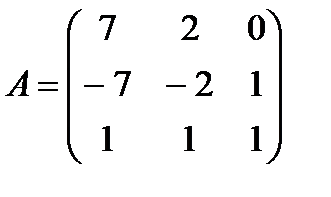 , , 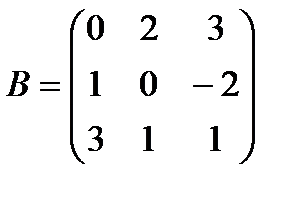 | ||
| Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. | 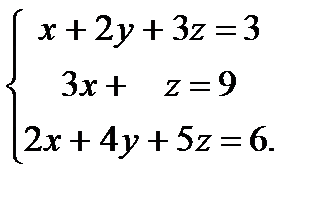 | ||
| Задание 3. Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему решений: | 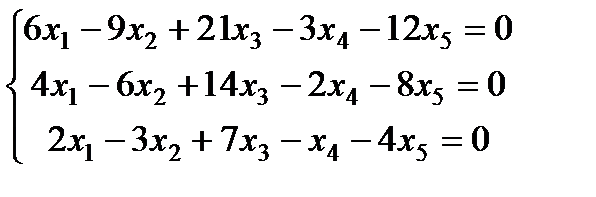 | ||
Задание 4. Найти угол между диагоналями параллелограмма, построенного на векторах
 2015-04-20
2015-04-20 2628
2628
