Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Определение
Пусть в некоторой окрестности точки 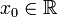 определена функция
определена функция 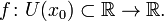 Производной функции называется такое число
Производной функции называется такое число 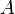 , что функцию в окрестности U (x 0) можно представить в виде
, что функцию в окрестности U (x 0) можно представить в виде
f (x 0 + h) = f (x 0) + Ah + o (h)
если 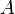 существует.
существует.
[править] Определение производной функции через предел
Пусть в некоторой окрестности точки 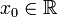 определена функция
определена функция 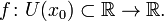 Производной функции f в точке x 0 называется предел, если он существует,
Производной функции f в точке x 0 называется предел, если он существует,
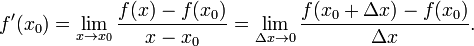
[править] Общепринятые обозначения производной функции y = f (x) в точке x 0
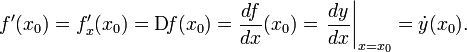
Заметим, что последнее обычно обозначает производную по времени
Дифференцируемость
Производная 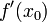 функции f в точке x 0, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x 0 тогда и только тогда, когда её производная в этой точке существует и конечна:
функции f в точке x 0, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x 0 тогда и только тогда, когда её производная в этой точке существует и конечна:
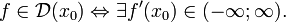
Для дифференцируемой в x 0 функции f в окрестности U (x 0) справедливо представление
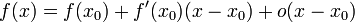 при
при 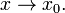
Производные высших порядков
Понятие производной произвольного порядка задаётся рекуррентно. Полагаем
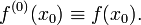
Если функция f дифференцируема в x 0, то производная первого порядка определяется соотношением
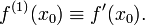
Пусть теперь производная n -го порядка f (n) определена в некоторой окрестности точки x 0 и дифференцируема. Тогда
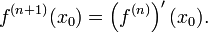
§ C ' = 0
§ x ' = 1
§ 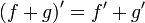 [2]
[2]
§ 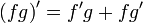 [3]
[3]
§ 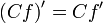
§ 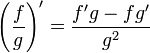 …(g ≠ 0)
…(g ≠ 0)
§ 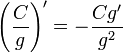 (g ≠ 0)
(g ≠ 0)
 2015-04-20
2015-04-20 1738
1738
