2015-04-20
10670
Цель: формирование умения раскрывать неопределенности вида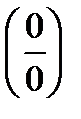 
и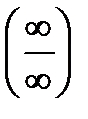 
при вычислении пределов функции.
Задание для самостоятельной внеаудиторной работы:
1.1. Выучите алгоритмы раскрытия неопределенностей вида 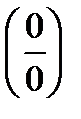и .
1.2. Найдите значение предела: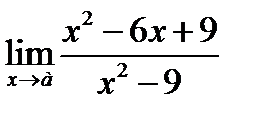 
, если: а) 
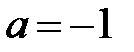, б)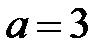 
1.3. Найдите значение предела: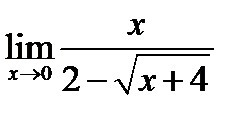 
1.4. Найдите значение предела: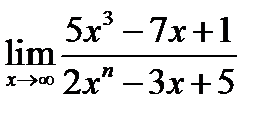 
, если: а) 
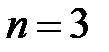, б) 
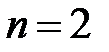, в)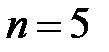 
1.5. Найдите предел: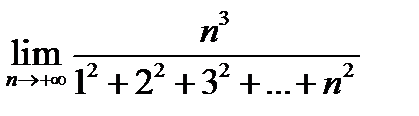 
Методические указания по выполнению работы:
- Предел функции в точке.
Вычисление пределов путем раскрытия неопределенности вида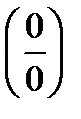 
.
Число b называется пределом функции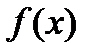 
при х, стремящемся к хо (или в точке хо), если для любого наперед заданного 
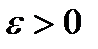существует такое 
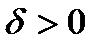, что для всех х, удовлетворяющих условиям 
, 
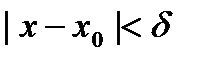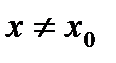, имеет место неравенство: 
.
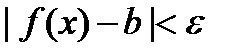Если b есть предел функци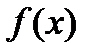и при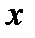 
→ 
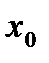то пишут: 
.
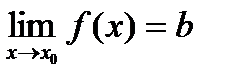При решении задач необходимо знание алгоритмов раскрытия неопределенностей:
раскрытие неопределенностей 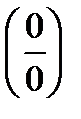при нахождении предела дробно-рациональных функций:
- разложить числитель или (и) знаменатель на множители,
- сократите дробь,
- вычислите предел.
раскрытие неопределенностей 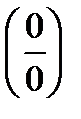при нахождении предела иррациональных функций:
- домножить числитель и знаменатель дроби на выражение, сопряженное числителю или (и) знаменателю,
- упростить выражение и сократить дробь,
3. вычислить предел.
Пример 1. Найдите предел: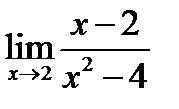 
.
Решение.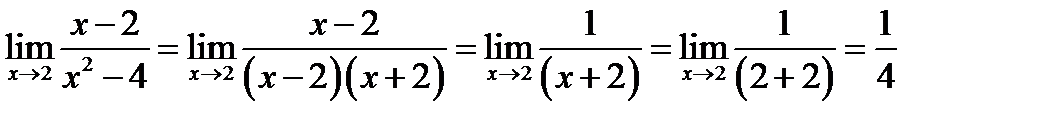 
Пример 2. Найдите предел: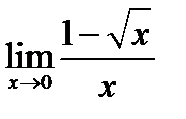 
.
Решение.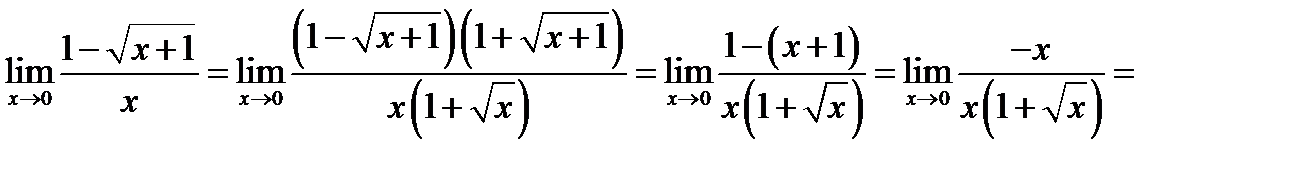 
= 
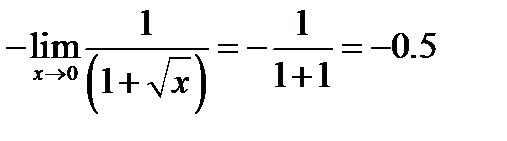
- Предел функции на бесконечности.
Вычисление пределов путем раскрытия неопределенности вида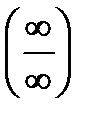 
.
Число b называется пределом функци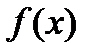и при 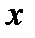→∞, если для любого наперед заданного 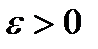существует такое 
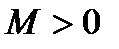, что для всех 
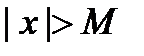имеет место неравенство: .
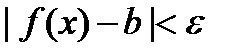Если b есть предел функци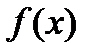и при 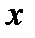→∞, то пишут: 
.
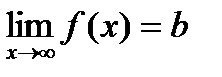Для нахождения пределов функций на бесконечности часто используют два основных предела: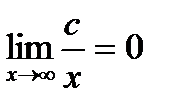 
и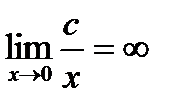 
, где с – константа.
Раскрытие неопределенностей при нахождении предела дробно-рациональных функций:
- делить числитель и знаменатель на переменную в большей степени,
- применить свойство бесконечно малых и бесконечно больших величин,
- вычислите предел.
Пример 3. Найдите предел: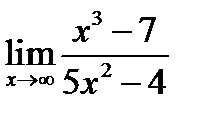 
Решение.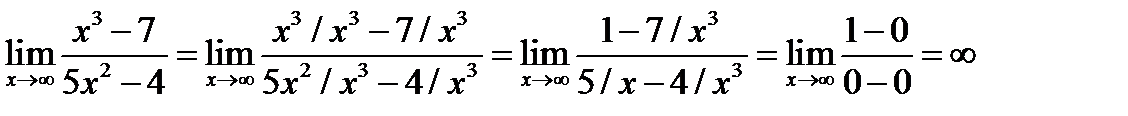 
Замечание: большая степень числителя превышает большую степень знаменателя, следовательно, предел стремится к бесконечности.
Пример 4. Найдите предел: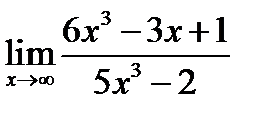 
Решение.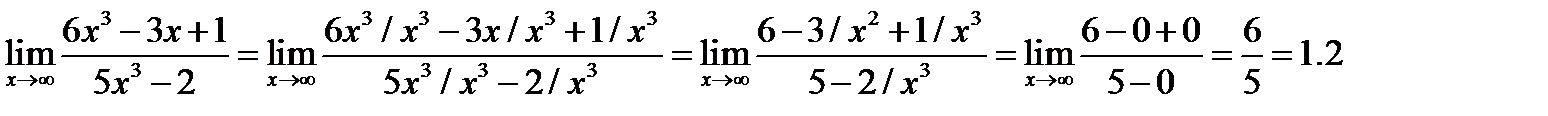 
Замечание: большая степень числителя совпадает с большей степенью знаменателя, следовательно, предел - отличное от нуля число.
Пример 5. Найдите предел: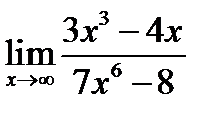 
Решение.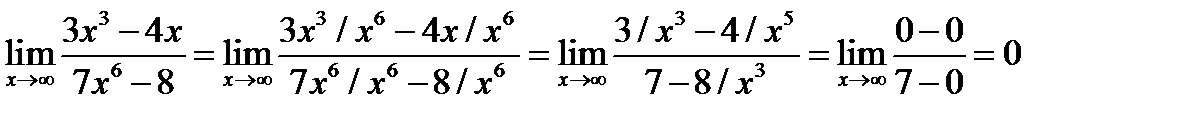 
Замечание: большая степень числителя меньше большей степени знаменателя, следовательно, предел равен нулю.
Список литературы:
1. Богомолов Н.В. Сергиенко Л.Ю. Сборник дидактических заданий по математике: Учебное пособие для ссузов Изд. 3-е,стереотип. Дрофа 2010 – Глава 6, § 1, стр. 76-80.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 6, § 31, стр. 188-198.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 4, §2, стр. 182 – 192.
