Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события A обозначается через P (A) и рассчитывается по формуле
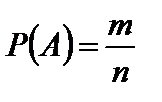 , (1)
, (1)
где m – число элементарных исходов, благоприятствующих событию A;
n – число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Вероятность события P (A) – численная мера, характеризующая степень возможности появления события A в данном испытании.
Вероятность достоверного события равна единице. Вероятность невозможного события равна нулю. Вероятность случайного события больше нуля и меньше единицы.
Вероятность любого события B удовлетворяет неравенствам:
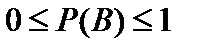 . (2)
. (2)
Пример 1.1. В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. Из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется голубым?
Решение. Обозначим событие «извлеченный шар окажется голубым» через A. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию A.
Вероятность события А рассчитывается по формуле (1) и будет равна
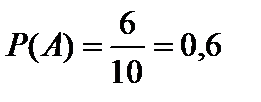 .
.
Пример 1.2. Найти вероятность того, что в наудачу выбранном двузначном числе цифры одинаковы.
Решение. Обозначим событие «число с одинаковыми цифрами» через А. Двузначными числами являются числа от 10 до 99. Всего таких чисел 90. Одинаковые цифры имеют 9 чисел (это числа 11, 22, 33, 44, 55, 66, 77, 88, 99). Так как в данном случае m = 9, n = 90, вероятность совпадения чисел будет равна
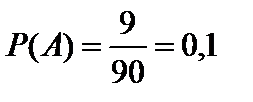 .
.
Числа m и n находят путем прямого перечисления элементарных исходов испытания. Однако, при большом числе элементарных исходов их перечисление весьма громоздко. Поэтому при подсчете числа элементарных исходов используют элементы комбинаторики.
Соединениями называют различные группы, составленные из каких-либо объектов, элементов. Различают три вида соединений: перестановки, размещения и сочетания.
Перестановками из n элементов называют соединения, содержащие все n элементов и отличающиеся между собой лишь порядком элементов. Число перестановок из n элементов находится по формуле
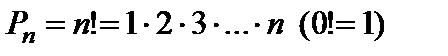 . (3)
. (3)
Например, 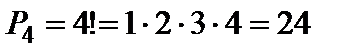 .
.
Размещениями из n элементов по k в каждом 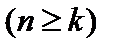 называют такие соединения, в каждое из которых входит k элементов, взятых из данных n элементов, и которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
называют такие соединения, в каждое из которых входит k элементов, взятых из данных n элементов, и которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
Число размещений из n элементов по k находят по формуле
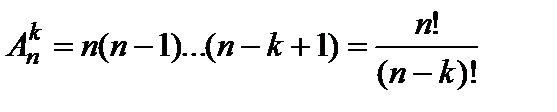 . (4)
. (4)
Например, 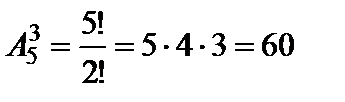 .
.
Сочетаниями из n элементов по 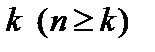 называют соединения, в каждое из которых входит k элементов, взятых из данных n элементов, и которые отличаются друг от друга, по крайней мере, одним элементом. Число сочетаний из n элементов по k находят по формуле
называют соединения, в каждое из которых входит k элементов, взятых из данных n элементов, и которые отличаются друг от друга, по крайней мере, одним элементом. Число сочетаний из n элементов по k находят по формуле
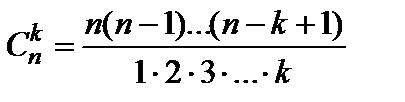 (5)
(5)
или
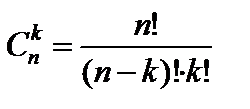 . (6)
. (6)
Например, 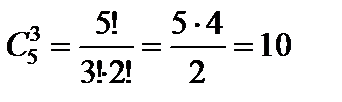 .
.
При вычислениях можно использовать следующее свойство сочетаний:
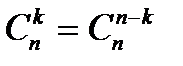 . (7)
. (7)
Число различных перестановок из 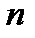 элементов, среди которых k 1 первого вида, k 2 – второго, …, km – m -го вида, определяется по следующей формуле:
элементов, среди которых k 1 первого вида, k 2 – второго, …, km – m -го вида, определяется по следующей формуле:
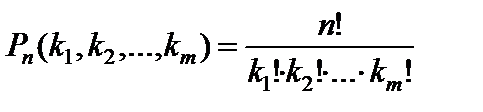 . (8)
. (8)
Число различных размещений по k элементов из n различных элементов, в которых каждый элемент может использоваться любое от
0 до k число раз исчисляется следующим образом:
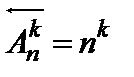 . (9)
. (9)
Число различных сочетаний по k элементов из n различных элементов, в которых каждый элемент может повторяться любое от
0 до k числа раз равно
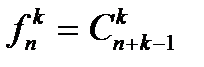 . (10)
. (10)
Пример 1.3. В студенческой группе, состоящей из 30 человек, нужно избрать актив группы (старосту, заместителя и профорга). Определите, сколькими способами это можно сделать.
Решение. Из множества 30 собравшихся человек нас интересу-
ют размещения из 30 по 3. Используя формулу (4) получим: 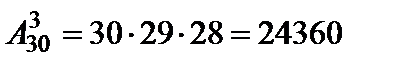 – столькими способами собрание может выбрать актив группы.
– столькими способами собрание может выбрать актив группы.
Пример 1.4. Рассчитать, сколькими различными способами могут разместиться на скамейке 5 человек.
Решение. Согласно формуле (3) при n = 5 находим: P 5 = 5! = 1 · 2 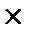
 3 · 4 · 5 = 120.
3 · 4 · 5 = 120.
Пример 1.5. Собранию из 30 человек надо выбрать 3 делегата на конференцию. Определите, сколькими способами это можно сделать.
Решение. Из множества в 30 человек надо выбрать подмножество в 3 человека. Для этого следует использовать формулу (6):
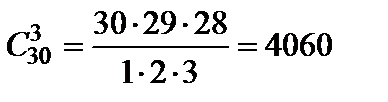 способами.
способами.
Пример 1.6. Из 15 билетов наудачу берется один. Какова вероятность того, что номер билета есть число, не делящееся ни на 3, ни на 5?
Решение. Обозначим через А событие «номер взятого билета не делится ни на 3, ни на 5». Всего элементарных исходов n = 15. Событию A благоприятствуют исходы 1; 2; 4; 7; 8; 11; 13; 14 (m = 8). Используя формулу (1) получим:
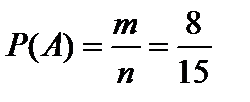 .
.
Пример 1.7. Бросили две игральные кости и подсчитали сумму
выпавших очков. Какова вероятность получить сумму, равную семи?
Решение. Событию A (сумма выпавших очков равна 7) благоприятствует следующих m = 6 исходов: (1;6), (2;5), (3;4), (5;2), (6;1).
Общее число исходов равно n = 36 (каждое из шести очков одной кости может выпасть в паре с любым из шести очков другой кости, следовательно, всех пар n = 6 · 6 = 36).
Используя формулу (1) получим:
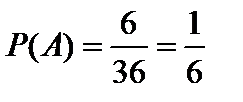 .
.
Пример 1.8. Наудачу взятый телефонный номер состоит из пяти цифр. Какова вероятность того, что в нем: 1) все цифры различны;
2) все цифры нечетны?
Решение.
1. Так как на каждом из пяти мест в пятизначном номере может стоять любая из цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, то всех пятизначных чисел будет 105. Номера, у которых все цифры различные, это размещения из 10 элементов по 5. Поэтому число благоприятствующих случаев равно 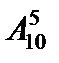 . Согласно формуле (1) искомая вероятность равна
. Согласно формуле (1) искомая вероятность равна
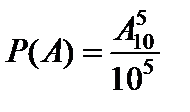 .
.
2. Из пяти нечетных цифр (1, 3, 5, 7, 9) можно образовать 55 различных пятизначных номеров. Так как всех равновозможных случаев 105, то искомая вероятность будет равна:
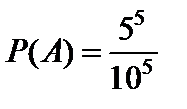 .
.
Пример 1.9. На пяти одинаковых карточках написаны буквы «л», «м», «о», «о», «т». Какова вероятность того, что:
1) извлекая все карточки по одной наугад, получим в порядке их выхода слово «молот»;
2) извлекая три карточки по одной наугад, получим в порядке выхода слово «том»?
Решение.
1. Пронумеруем буквы в том порядке, в котором они написаны:
| л | м | о | о | т | ||||||
Из пяти различных букв можно составить 120 перестановок (P 5 =
= 1 · 2 · 3 · 4 · 5 = 120), значит общее число равновозможных исходов равно n = 120. Событие A (получится слово «молот») произойдет, если карточки будут взяты в следующем порядке:
| или | ||||||||||
| м | о | л | о | т | м | о | л | о | т |
Благоприятствующих исходов событию А m = 2, следовательно искомая вероятность равна:
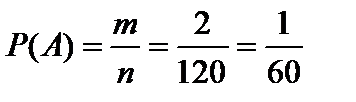 .
.
2. Общее число исходов равно 60 (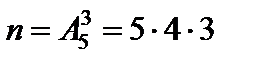 ). Слово «том» появится, если карточки будут взяты в следующем порядке:
). Слово «том» появится, если карточки будут взяты в следующем порядке:
| или | ||||||
| т | о | м | т | о | м |
Благоприятствующих исходов событию B (получено слово «том») будет два, т. е. m = 2. Следовательно, вероятность события В равна
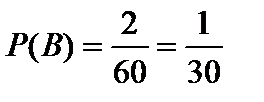 .
.
Пример 1.10. Из колоды в 36 карт наугад вынимаются 3 карты. Какова вероятность того, что среди них окажутся два туза?
Решение. Обозначим событие «среди трех карт два туза» через A. Общее число возможных исходов 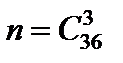 . Определим число исходов, благоприятствующих событию A.
. Определим число исходов, благоприятствующих событию A.
Два туза из четырех можно взять 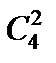 способами, еще одну любую карту можно взять
способами, еще одну любую карту можно взять 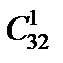 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 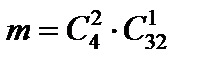 и вероятность события А составит
и вероятность события А составит
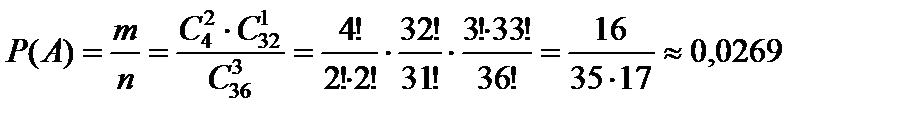 .
.
 2015-04-20
2015-04-20 7068
7068
