Непрерывной называют такую случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Вероятность того, что непрерывная случайная величина X примет значение C, равна нулю (P (X = C) = 0), так как это есть вероятность того, что из бесконечного множества значений выпадает наперед заданное. Следовательно, значениям X в этом случае нельзя ставить в соответствии их вероятности. Закон распределения непрерывной величины Х может быть задан с помощью функции распределения:
F (x) = P (– 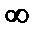 < X < x). (50)
< X < x). (50)
Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:
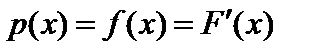 . (51)
. (51)
Плотность распределения называют также дифференциальной функцией распределения. Зная плотность распределения, можно найти функцию распределения
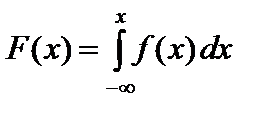 . (52)
. (52)
Плотность распределения вероятностей обладает следующими свойствами:
1. 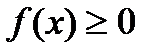 . (53)
. (53)
2. 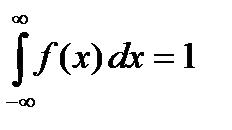 . (54)
. (54)
3. 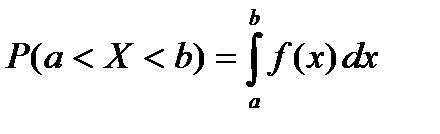 . (55)
. (55)
4. 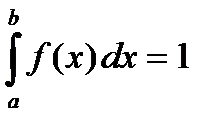 , если
, если 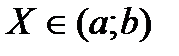 . (56)
. (56)
График дифференцируемой функции называют кривой распределения. Дифференциальная функция существует только для непрерывных случайных величин, а интегральная как для непрерывных, так и для дискретных случайных величин. Функция f (x) вероятностью не является.
Пример 2.11. Плотность распределения случайной величины X задана функцией 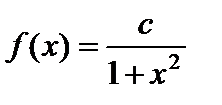 . Найти значение параметра c.
. Найти значение параметра c.
Решение. Используя формулу (54) получим:
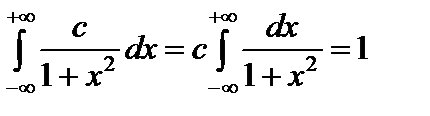 ;
; 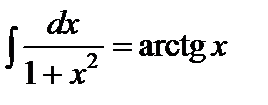 ;
;
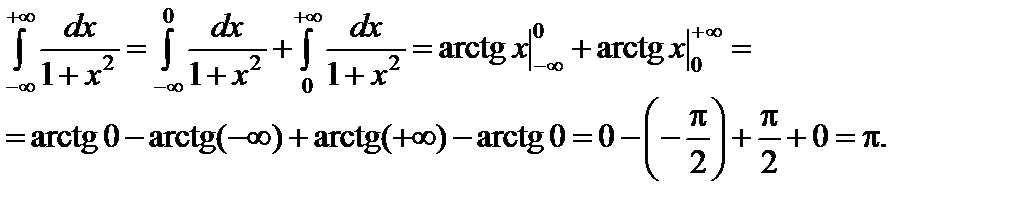
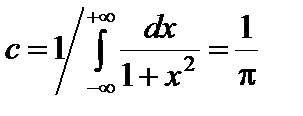 ;
; 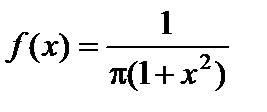 .
.
Пример 2.12. Найти вероятность того, что в результате испытания случайная величина X примет значение из интервала (1;2), если плотность вероятности величины X задана следующей функцией:
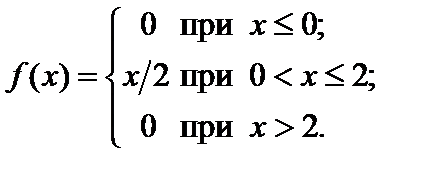
Решение. 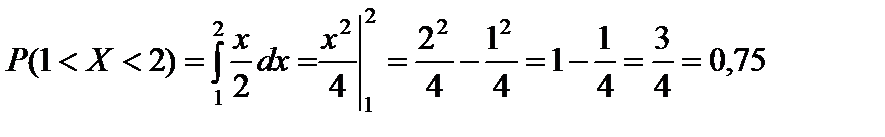 .
.
Пример 2.13. Найти плотность распределения случайной величины X, функция распределения которой имеет вид:
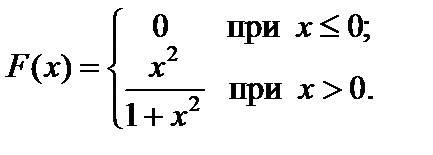
Решение. 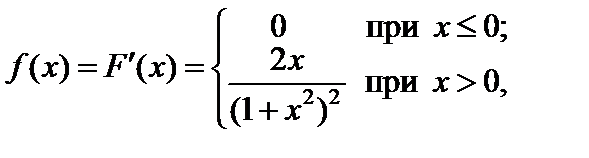
где 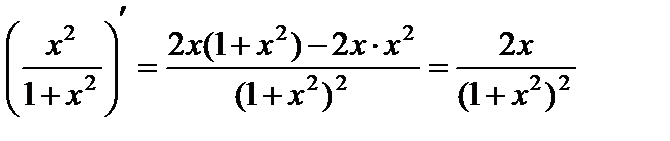 .
.
Пример 2.14. Найти функцию распределения F (x), если плотность распределения случайной величины X равна:
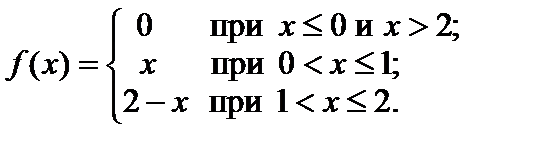
Решение. Используя формулу (52) получим:
· при 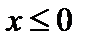
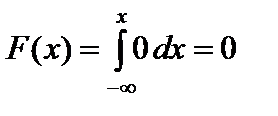 ;
;
· при 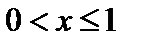
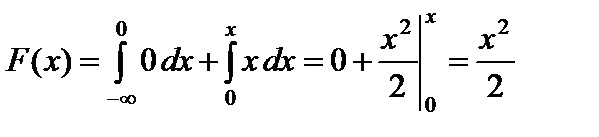 ;
;
· при 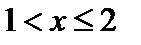
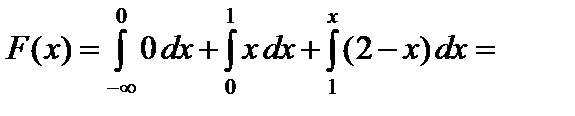
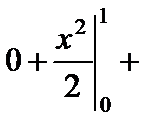
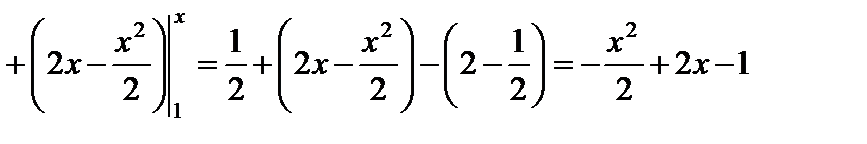 .
.
Искомая функция распределения имеет вид: x > 2,
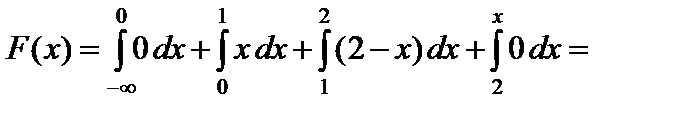
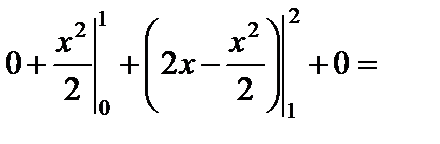
= 0,5 + 4 – 2 – 2 + 0,5 + 0 = 1.
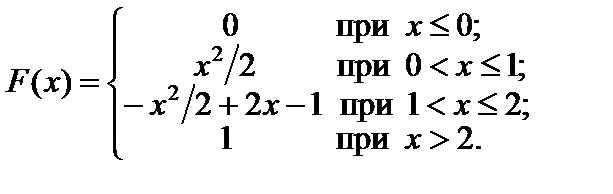 .
.
Графики функций f (x) и F (x) отражены на рис. 2.3 и 2.4.
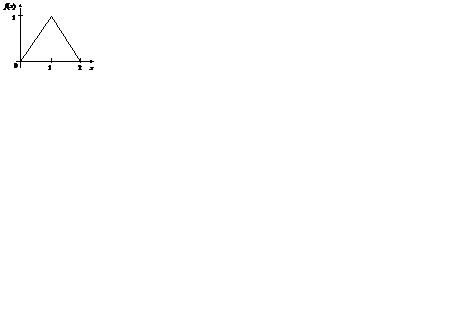 Рис. 2.3 Рис. 2.3 | 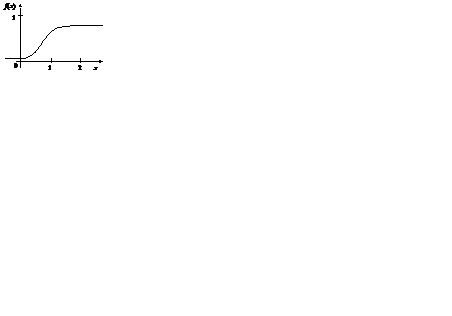 Рис. 2.4 Рис. 2.4 |
 2015-04-20
2015-04-20 723
723







