Доказательство

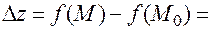
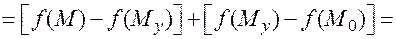
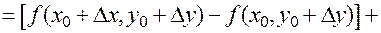
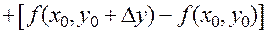
(см. рис. 7).

Разность

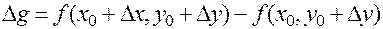
можно рассматривать как разность двух значений функции

,

зависящей от одной переменной 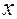, причем ее производная является частной производной по 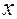исходной функции 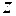: 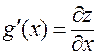. По теореме Лагранжа [4]:

,

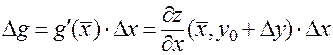где промежуточная точка 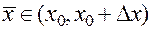, и потому .

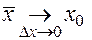Аналогично разность

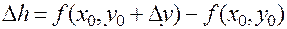
можно рассматривать как разность двух значений функции 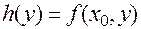, зависящей от одной переменной 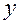, причем ее производная является частной производной по 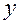исходной функции 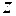: 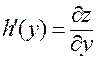. По теореме Лагранжа:

,

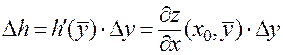где промежуточная точка 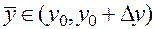, и потому .

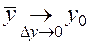Итак,

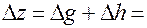
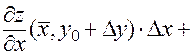
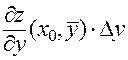. (5)

Воспользуемся теперь непрерывностью частных производных в точке :

.

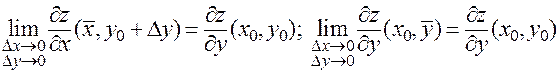Отсюда по теореме о структуре сходящейся переменной [4]):

;

,

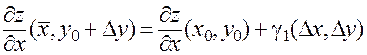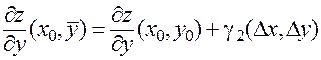где функции 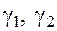являются бесконечно малыми величинами пр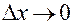и и 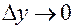. Подставляя эти выражения в (5), получаем (4). ▄