Напомним, что для функции одной переменной 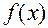 дифференцируемость в точке
дифференцируемость в точке 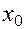 по определению означает существование конечного предела
по определению означает существование конечного предела
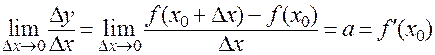 .
.
Необходимым и достаточным условием для этого является возможность представления приращения 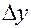 в точке
в точке 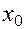 в виде:
в виде:
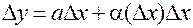 , (1)
, (1)
где 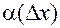 является бесконечно-малой величиной; при этом
является бесконечно-малой величиной; при этом 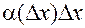 является, как функция переменной
является, как функция переменной 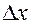 , бесконечно малой величиной более высокого порядка, чем
, бесконечно малой величиной более высокого порядка, чем 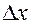 [4].
[4].
В случае функции нескольких переменных в основу понятия дифференцируемости кладется условие, аналогичное (1).
Итак, пусть функция 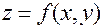 определена в окрестности точки
определена в окрестности точки 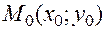 .
.
Определение. Функция 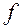 называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее полное приращение в этой точке
, если ее полное приращение в этой точке 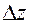 , как функция аргументов
, как функция аргументов 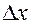 и
и 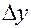 , представимо в виде:
, представимо в виде:
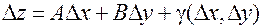 , (2)
, (2)
где функция 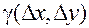 является при
является при 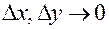 бесконечно малой величиной более высокого порядка, чем
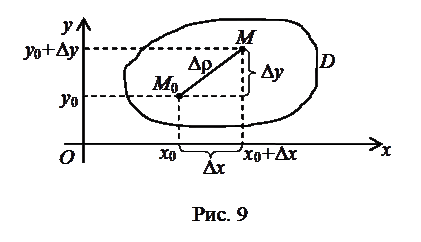
бесконечно малой величиной более высокого порядка, чем 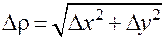 (рис. 9).
(рис. 9).
В этом случае выражение 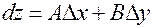 , являющееся линейной функцией аргументов
, являющееся линейной функцией аргументов 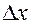 и
и 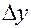 , называется полным дифференциалом функции
, называется полным дифференциалом функции 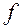 в точке
в точке  .
.
 |
Замечание. Из дифференцируемости функции
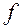 в точке
в точке  следует ее непрерывность в этой точке, поскольку из (2) следует:
следует ее непрерывность в этой точке, поскольку из (2) следует: 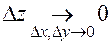 .
. Теорема. Если функция 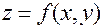 дифференцируема в точке
дифференцируема в точке  , то в этой точке существуют частные производные, и коэффициенты
, то в этой точке существуют частные производные, и коэффициенты 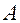 и
и 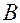 в формуле (2) равны их значениям:
в формуле (2) равны их значениям:
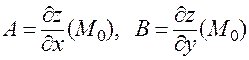 .
.
Доказательство. Положим в формуле (2) 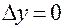 и устремим
и устремим 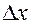 к нулю. При этом
к нулю. При этом 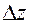 становится частным приращением
становится частным приращением 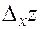 , и (2) принимает вид:
, и (2) принимает вид:
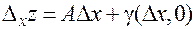 ,
,
откуда
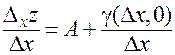 , (3)
, (3)
причем
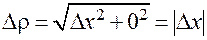 ,
,
так что в соответствии с условием на 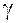 и ввиду ограниченности величины
и ввиду ограниченности величины 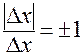 :
:
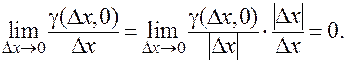
Переходя в равенстве к пределу при 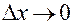 , получаем:
, получаем: 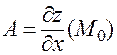 .
.
Аналогично устанавливается равенство 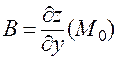 . ▄
. ▄
Таким образом, полный дифференциал имеет вид:
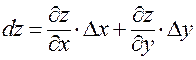 .
.
Из формулы (2) следует, что при малых по модулю 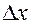 и
и 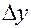 имеет место приближенное равенство полного приращения и полного дифференциала, которые отличаются на бесконечно малую величину
имеет место приближенное равенство полного приращения и полного дифференциала, которые отличаются на бесконечно малую величину 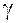 более высокого порядка, чем
более высокого порядка, чем 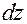 и
и 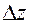 .
.
 2015-05-14
2015-05-14 2488
2488








