Пусть функция 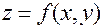 задана в области
задана в области 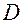 , содержащей точку
, содержащей точку  .
.
Определение. 1. Точка  называется точкой максимума функции
называется точкой максимума функции 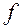 , если для всех точек
, если для всех точек 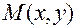 из некоторой окрестности точки
из некоторой окрестности точки  выполняется неравенство
выполняется неравенство 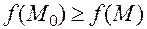 (другими словами, точка
(другими словами, точка  является для этой окрестности точкой наибольшего значения).
является для этой окрестности точкой наибольшего значения).
2. Аналогично точка  называется точкой минимума функции
называется точкой минимума функции 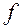 , если для всех точек
, если для всех точек 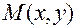 из некоторой окрестности выполняется неравенство
из некоторой окрестности выполняется неравенство 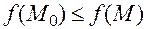 .
.
|
Точки максимума и минимума называют точками экстремума.
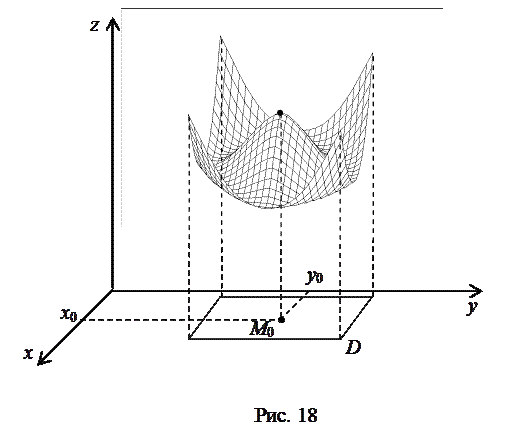
Замечание. Понятие точки экстремума является локальной характеристикой функции, говорящей о ее поведении в малой окрестности точки  . В точках, далеких от
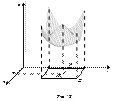
. В точках, далеких от  , значения функции могут быть больше, чем в точке максимума или меньше, чем в точке минимума (рис. 18).
, значения функции могут быть больше, чем в точке максимума или меньше, чем в точке минимума (рис. 18).
 |
Необходимое условие экстремума
Теорема. Если функция 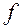 имеет в точке
имеет в точке  экстремум, то каждая из частных производных
экстремум, то каждая из частных производных 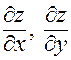 , если она существует в этой точке, равна нулю.
, если она существует в этой точке, равна нулю.
Таким образом, необходимое условие экстремума в точке  в случае существования частных производных имеет вид:
в случае существования частных производных имеет вид:
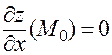 ;
; 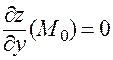 .
.
Доказательство. Пусть например,  — точка максимума, и в этой точке существует частная производная
— точка максимума, и в этой точке существует частная производная 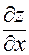 . Зафиксируем
. Зафиксируем 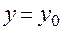 и рассмотрим функцию одной переменной
и рассмотрим функцию одной переменной 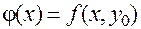 . Тогда
. Тогда 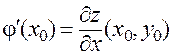 . Из определения точки экстремума следует, что
. Из определения точки экстремума следует, что 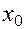 является для функции
является для функции 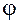 точкой максимума, и необходимое условие экстремума для функции одной переменной дает:
точкой максимума, и необходимое условие экстремума для функции одной переменной дает: 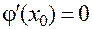 , то есть
, то есть 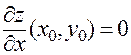 .
.
Определение. Точка  области определения функции
области определения функции 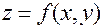 называется стационарной, если в этой точке существуют частные производные первого порядка, и выполняется необходимое условие экстремума:
называется стационарной, если в этой точке существуют частные производные первого порядка, и выполняется необходимое условие экстремума:
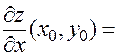
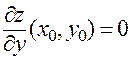 .
.
 2015-05-14
2015-05-14 474
474