Достаточное условие экстремума

Теорема. Пусть в окрестности стационарной точки 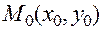функция 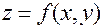имеет частные производные до третьего порядка включительно. Обозначим:

; ; ; .

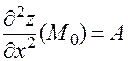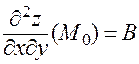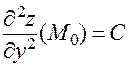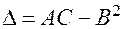Тогда:

1. Если 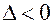, то в точке экстремума нет.

2. 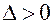, то в точке имеется экстремум; при этом:

если 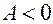, то — точка максимума;

если 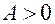, то — точка минимума.

(без доказательства).

Замечание. Если 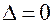, то для решения вопроса о наличии экстремума требуется привлечение производных более высоких порядков.

Пример. Рассмотрим функцию

.

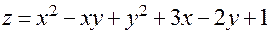Здесь

; .

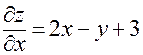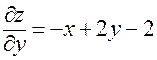Решая систему уравнений, находим стационарные точки путем решения системы уравнений:

.

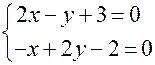Функция имеет единственную стационарную точку 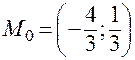. Находим частные производные второго порядка:

; ; .

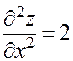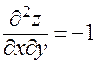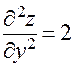Далее, 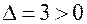, и 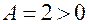. Значит, 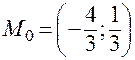— точка минимума.