Напомним, что плоскость 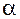 , проходящая через точку
, проходящая через точку 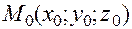 и перпендикулярная нормальному вектору
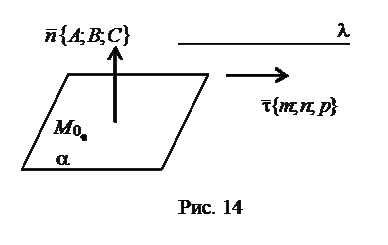
и перпендикулярная нормальному вектору 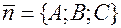 (рис. 14), задается уравнением:
(рис. 14), задается уравнением:
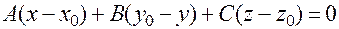 .
.
Напомним далее, что условие параллельности плоскости 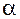 и пространственной прямой
и пространственной прямой 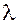 , заданной каноническими уравнениями
, заданной каноническими уравнениями
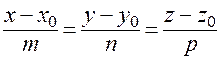 ,
,
имеет вид:
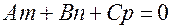 .
.
Определение. Прямая 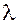 называется касательной прямой к поверхности
называется касательной прямой к поверхности 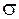 в точке
в точке  , если она является касательной в точке
, если она является касательной в точке  к какой-либо кривой
к какой-либо кривой 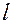 , лежащей на поверхности
, лежащей на поверхности 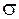 (рис. 15).
(рис. 15).

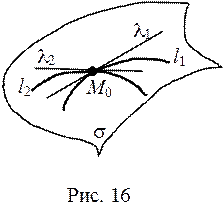
Заметим что через точку  можно провести разные кривые
можно провести разные кривые 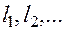 и получить, соответственно, разные касательные прямые
и получить, соответственно, разные касательные прямые 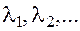 к поверхности
к поверхности 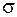 (рис. 16).
(рис. 16).
Пусть поверхность  задана уравнением
задана уравнением 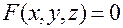 .
.
Определение. Точка 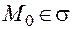 называется обыкновенной точкой поверхности
называется обыкновенной точкой поверхности 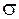 , если выполняются три условия:
, если выполняются три условия:
1. В окрестности точки  существуют частные производные
существуют частные производные 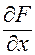 ,
,  ,
,  .
.
2. В точке  частные производные непрерывны.
частные производные непрерывны.
3. В точке  частные производные не обращаются одновременно в нуль.
частные производные не обращаются одновременно в нуль.
Теорема. Все касательные прямые к поверхности 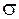 в неособенной точке
в неособенной точке  лежат в одной плоскости.
лежат в одной плоскости.
Доказательство. Пусть 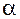 — плоскость, проходящая через точку
— плоскость, проходящая через точку  и имеющая нормальный вектор
и имеющая нормальный вектор
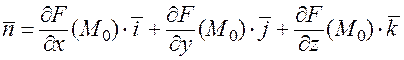
(вектор 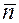 является ненулевым поскольку точка
является ненулевым поскольку точка  по условию неособенная). Покажем, что в плоскости
по условию неособенная). Покажем, что в плоскости 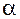 лежит любая касательная прямая
лежит любая касательная прямая 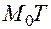 . Пусть эта прямая является касательной к линии
. Пусть эта прямая является касательной к линии 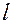 , имеющей параметрические уравнения
, имеющей параметрические уравнения
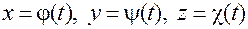 ,
,
и
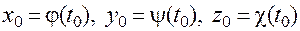 .
.
Канонические уравнения касательной к линии 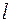 имеют вид:
имеют вид:
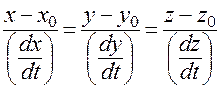 .
.
Направляющий вектор касательной 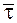 имеет координаты:
имеет координаты:
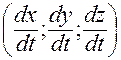 .
.
Достаточно показать, что векторы 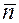 и
и 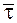 перпендикулярны; необходимым и достаточным условием для этого является равенство нулю скалярного произведения:
перпендикулярны; необходимым и достаточным условием для этого является равенство нулю скалярного произведения: 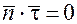 . Имеем:
. Имеем:
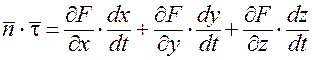 ;
;
правая часть здесь является полной производной 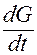 сложной
сложной 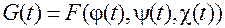 ; при этом функция
; при этом функция 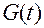 при всех
при всех 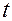 тождественно равна нулю, поскольку точка
тождественно равна нулю, поскольку точка 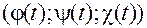 лежит на поверхности, и, следовательно, ее координаты удовлетворяют уравнению
лежит на поверхности, и, следовательно, ее координаты удовлетворяют уравнению 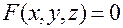 ). Итак,
). Итак,
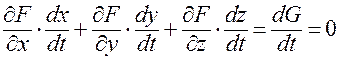 . ▄
. ▄
Определение. Плоскость 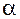 , в которой лежат все касательные прямые к поверхности
, в которой лежат все касательные прямые к поверхности 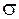 в неособенной точке
в неособенной точке  , называется касательной плоскостью к поверхности.
, называется касательной плоскостью к поверхности.
Пример. Найдем уравнение касательной плоскости к поверхности, заданной уравнением 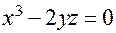 в точке
в точке 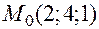 . Здесь
. Здесь 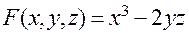 . Вычислим частные производные функции
. Вычислим частные производные функции 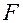 :
:
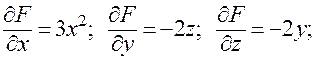
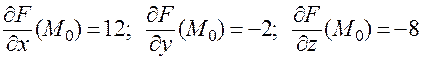 .
.
Уравнение касательной плоскости:
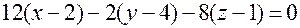 .
.
Уравнения нормали к поверхности
 |
Определение. Прямая
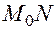 , проходящая через точку
, проходящая через точку  поверхности
поверхности 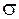 перпендикулярно касательной плоскости
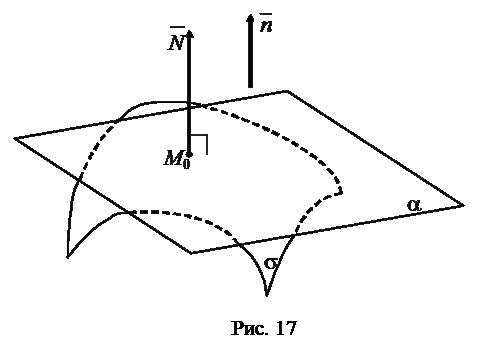
перпендикулярно касательной плоскости 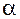 , называется нормалью к поверхности в точке
, называется нормалью к поверхности в точке  (рис. 17).
(рис. 17). Направляющий вектор нормали 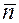 совпадает с нормальным вектором касательной плоскости:
совпадает с нормальным вектором касательной плоскости:
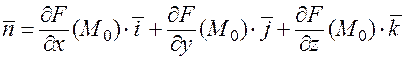 .
.
Поэтому канонические уравнения нормали к поверхности имеют вид:
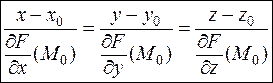
В последнем примере канонические уравнения нормали имеют вид:
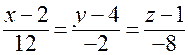 .
.
 2015-05-14
2015-05-14 3567
3567
