Определение. Касательной к линии 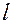 в точке
в точке  называется предельное положение секущей
называется предельное положение секущей 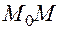 при
при 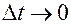 .
.
Это предельное положение определяется предельными значениями переменных величин, входящих в уравнения секущей 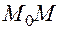 . Последняя задается каноническими уравнениями:
. Последняя задается каноническими уравнениями:
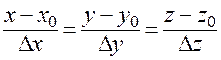 .
.
Разделим знаменатели всех членов равенства на 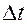 :
:
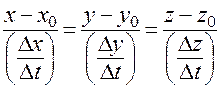 . (23)
. (23)
Поскольку

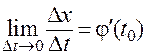 ,
, 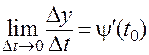 ,
, 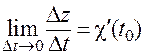 ,
,
то, переходя в (23) к пределу при 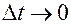 , получаем уравнения касательной
, получаем уравнения касательной 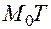 :
:
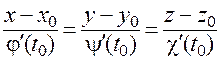 ,
,
или
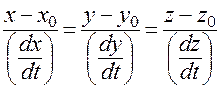 .
.
Пример. Найдем канонические уравнения касательной к линии, заданной параметрическими уравнениями:
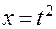 ;
; 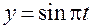 ;
; 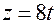
в точке 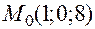 , соответствующей значению параметра
, соответствующей значению параметра 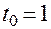 .
.
Находим производные:
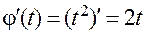 ;
; 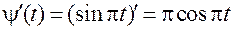 ;
; 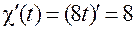 .
.
Полагая здесь 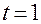 , получаем канонические уравнения касательной в точке
, получаем канонические уравнения касательной в точке  :
:
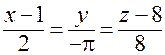 .
.
 2015-05-14
2015-05-14 449
449








