 |
Напомним, что для ненулевого вектора
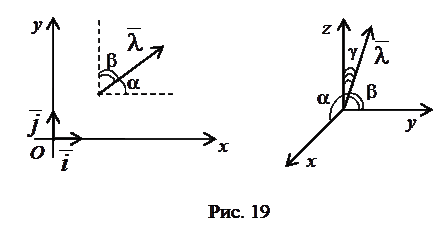
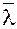 плоскости или пространства его направляющими косинусами называются косинусы углов, которые этот вектор образует с осями декартовой системы координат (рис. 19).
плоскости или пространства его направляющими косинусами называются косинусы углов, которые этот вектор образует с осями декартовой системы координат (рис. 19).
Если ненулевой вектор плоскости 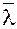 имеет в ортонормированном базисе, связанном с этой системой, координаты
имеет в ортонормированном базисе, связанном с этой системой, координаты 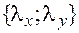 , то есть
, то есть 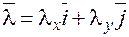 , то
, то
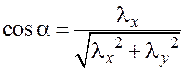 ;
; 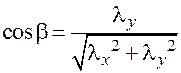 .
.
Аналогично в случае ненулевого вектора пространства 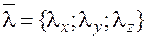 формулы для направляющих косинусов имеют вид:
формулы для направляющих косинусов имеют вид:
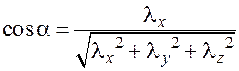 ;
; 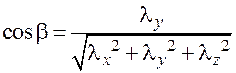 ;
;
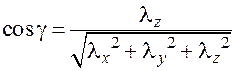 .
.
Направляющие косинусы вектора задают его направление в пространстве. Вектор 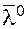 , координатами которого являются направляющие косинусы вектора
, координатами которого являются направляющие косинусы вектора 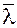 , сонаправлен с вектором
, сонаправлен с вектором 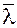 и имеет модуль, равный единице (рис. 20).
и имеет модуль, равный единице (рис. 20).
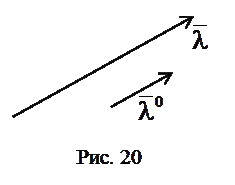 |
 2015-05-14
2015-05-14 657
657








