2015-05-14
1246
Пусть функция двух переменных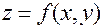 
имеет в области 
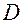частные производные 
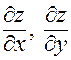, и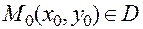 
.
Определение. Градиентом функции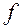 
в точке 
называется вектор grad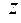 
, координатами которого являются значения частных производных в этой точке:
grad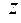 
.
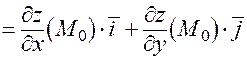Пример. Пусть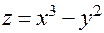 
. Тогда
; 
;
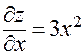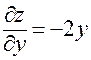grad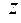 
.
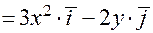В точке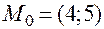 
:
grad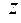 
.
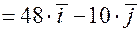Аналогичным образом определяется градиент в случае функции большего числа переменных. Например, для функции трех переменных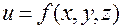 
:
grad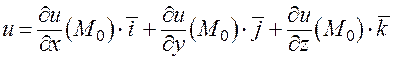 
. (28)
