2015-05-14
445
Содержание
| Глава I. | Приближенное решение уравнений......................................................................... | |
| §1. | Отделение корней уравнений....................................................................................... | |
| §2. | Правило пропорциональных частей (метод хорд)..................................................... | |
| §3. | Метод касательных (Ньютона)..................................................................................... | |
| §4. | Комбинированное применение методов хорд и касательных................................... | |
| §5. | Метод итераций............................................................................................................ | |
| Упражнения.................................................................................................................... | ||
| Глава II. | Интерполирование функций..................................................................................... | |
| §1. | Интерполяционный полином Лагранжа...................................................................... | |
| §2. | Интерполяционная формула Ньютона........................................................................ | |
| Упражнения.................................................................................................................... | ||
| Глава III. | Приближенные вычисления определенных интегралов..................................... | |
| §1. | Метод прямоугольников............................................................................................... | |
| §2. | Метод трапеций............................................................................................................. | |
| §3. | Метод парабол (Метод Симпсона).............................................................................. | |
| Упражнения.................................................................................................................... | ||
| Глава IV. | Приближенное решение дифференциальных уравнений.................................... | |
| §1. | Метод Эйлера................................................................................................................. | |
| §2. | Метод Рунге – Кутта..................................................................................................... | |
| Упражнения.................................................................................................................... | ||
| Литература........................................................................................................................................... |
ГЛАВА 1
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ.
Отделение корней уравнения.
Корнем уравнения
f (x) = 0 (1)
называется такое значение х = х0 при котором уравнение (1) превращается в тождество:
f (x0 ) = 0
Корень уравнения геометрически представляет собой абсциссу точки пересечения, касания или другой общей точки графика функции у = f(x) и оси ОХ (рис.1.1).
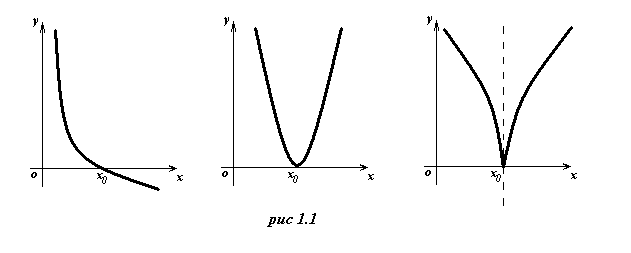
Отделить корень уравнения – значит найти такой конечный промежуток, внутри которого имеется единственный корень данного уравнения.
