Правило пропорциональных частей (метод хорд)

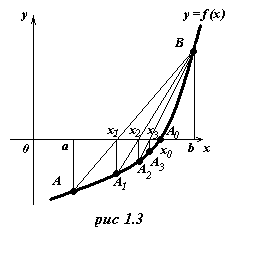
Метод хорд приближенного решения уравнения (1) имеет следующую геометрическую иллюстрацию: вместо точки пересечения оси ОХ и графика функции у = f(x), входящей в это уравнение, рассматривается точка пересечения данной оси и отрезка прямой, соединяющей концы дуги графика. Пусть требуется вычислить действительный корень уравнения f(x) = 0, изолированный на отрезке [a; b]. Рассмотрим график функции у = f(x). Пусть f (a) < 0, а f(b) > 0.

Точки А (a; f (a)) и В (b; f(b)) соединим хордой. Найдем точку х_{1 :}

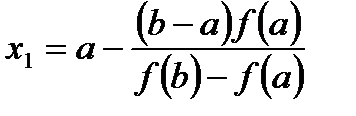(3)

Если f (х₁) < 0, то за новый, более узкий, интервал изоляции можно взять отрезок[ х₁; b]. Соединив точки А₁ (х₁; f (х₁)) и В (b; f(b)), получим в точке пересечения хорды с осью второе приближение х₂, которое вычислим по формуле:

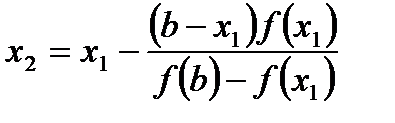(4)

и т. д. Последовательность чисел а, х₁, х₂.... стремится к искомому корню х₀. Вычисления следует вести до тех пор, пока не перестанут изменяться те десятичные знаки, которые мы хотим сохранить в ответе (т.е. пока не будет достигнута заданная степень точности).

Пример 1.2:

Методом хорд найти положительный корень уравнения х⁴ - 2х – 4 = 0 с точностью до 0,01

Решение. Положительный корень будет находиться в промежутке (1; 1,7), т.к. f (1) = -5<0, а

f (1,7) = 0,952 > 0. Найдем первое приближенное значение корня по формуле (3):

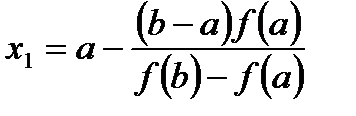, где а = 1, b=1,7

Получим 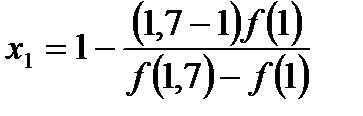=1,588

Так как f (1,588) = -0,817 < 0, то применяя вторично способ хорд к промежутку (1,588; 1,7) получим: 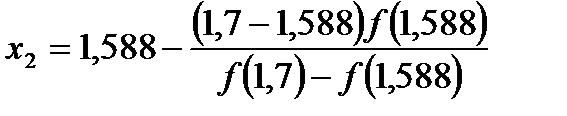= 1,639; f (1,639) = -0,051 < 0.

Найдем третье приближенное значение на промежутке (1,639; 1,7)

получим: 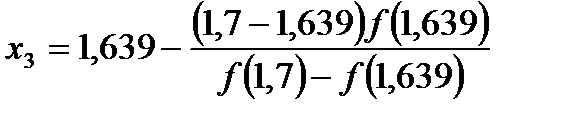= 1,642; f (1,642) = -0,016 < 0.

Найдем четвертое приближенное значение на отрезке (1,642; 1,7)

получим: 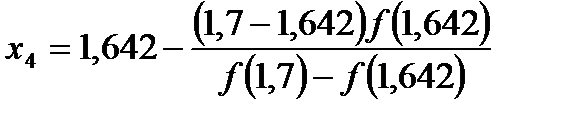= 1,643; f (1,643) =-0,004>0.

Следовательно, искомый корень с точностью до 0,01 равен 1,64