2015-05-14
674
Метод касательных отличается от метода хорд тем, что здесь рассматривается не секущая, соединяющая концы дуги графика, а касательная к графику. Точка пересечения касательной с осью ОХ дает приближенное значение корня.
Пусть действительный корень уравнения f(x) = 0 изолирован на отрезке [a; b]. Выберем на отрезке [a; b] такое число х0, при котором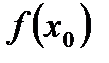 
имеет тот же знак что и 
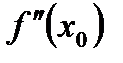, т.е. выполняется условие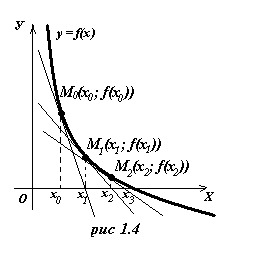 
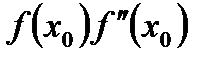>0 (5)
Проведем в точке М0 (х0; 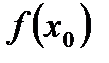) касательную к кривой
у = f(x). За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью ОХ. Это приближенное значение корня найдется по формуле:
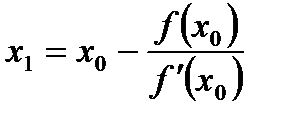(6)
Применив этот метод вторично в точке М1 (х1;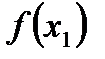 
), получим:
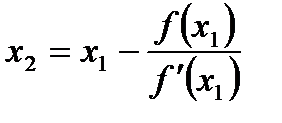(7)
и т.д. Полученная таким образом последовательность х0, х1, х2.... имеет своим пределом искомый корень.
Пример 1.3:
Методом касательных найти положительный корень уравнения х4 - 2х – 4 = 0 с точностью до 0,01
Решение. Здесь f(x) = х4 - 2х – 4,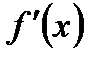 
=4х3 – 2, 
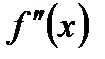= 12х2. Так как f(x) и 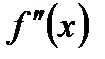при х0=1,7 имеют один и тот же знак, а именно: f (1,7) = 0,952 > 0 и 
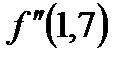= 34,68> 0, то применяя формулу 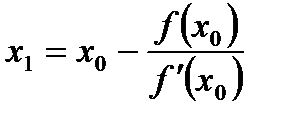где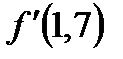 
=17,652. Тогда 
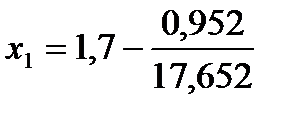= 1,646.
Применяя второй раз способ касательных, получим: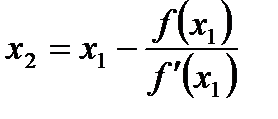 
, где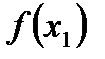 
= 
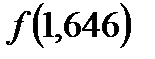= 0,048, 
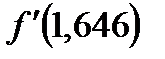=15,838. 
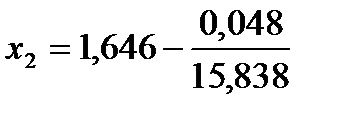= 1,643.
Аналогично получим третье приближение:
, 
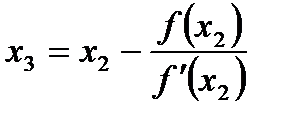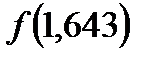=0,004, 
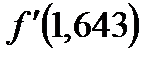=15,740, следовательно, 
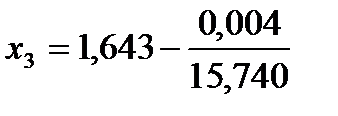= 1,6427.
Следовательно, искомый корень с точностью до 0,01 равен 1,64
