Метод прямоугольников

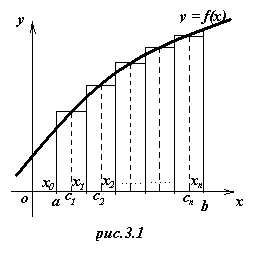
Пусть на отрезке [a; b], где a < b, задана непрерывная функция f(x). Требуется вычислить интеграл 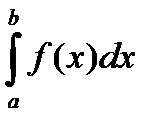, численно равный площади соответствующей криволинейной трапеции. Разобьем основание этой трапеции на п равных частей длины 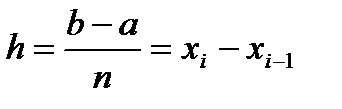. тогда x_i = x₀+hi. В середине 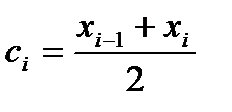каждого такого отрезка построим ординату 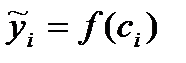графика функции у = f(x). Приняв эту ординату за высоту построим прямоугольник с площадью

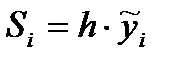. Тогда сумма площадей всех п прямоугольников (при достаточно большом п) дает площадь приближенно равную площади трапеции, т.е.

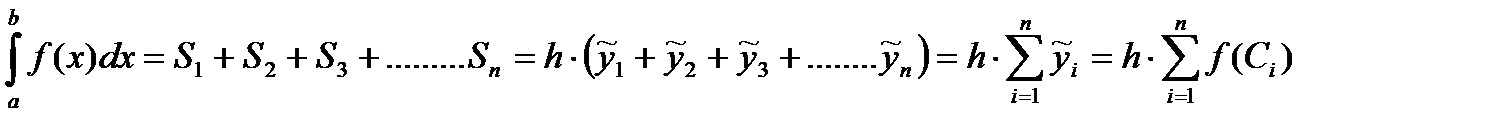
т.е.

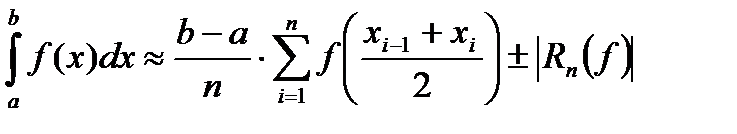- формула прямоугольников (1)

Абсолютная погрешность метода определяется неравенством:

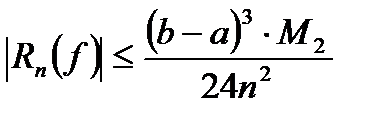(2)

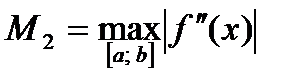где (3)

Пример 3.1: Вычислить интеграл 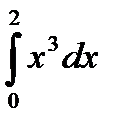при п = 4, используя метод прямоугольников.