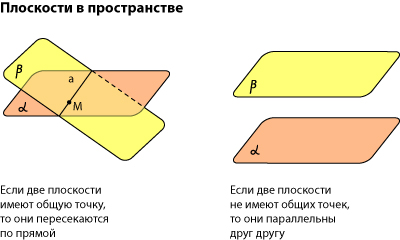
Плоскости могут совпадать, быть параллельными или пересекаться по прямой.
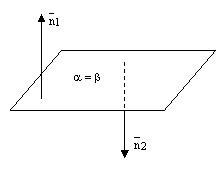
рис.3.
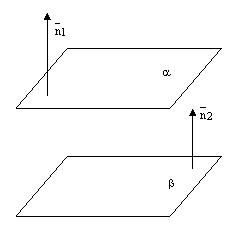
рис.4.
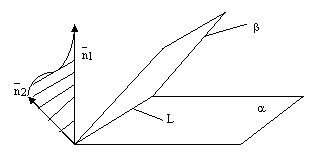
рис.5.
Признаки параллельности прямой и плоскости:
1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
18. Взаимные расположения плоскостей в пространстве. Параллельность плоскостей.
Плоскость, прямая, точка — основные понятия геометрии. Нам трудно дать им четкие определения, однако интуитивно мы понимаем, что это такое. Плоскость имеет только два измерения. У нее нет глубины. Прямая имеет лишь одно измерение, а у точки вообще нет размеров — ни длины, ни ширины, ни высоты.
Плоскость бесконечна. Поэтому в задачах мы рисуем только часть плоскости. Надо же как-то ее изобразить.
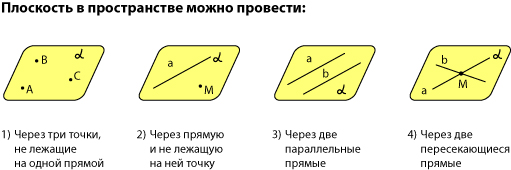
Две плоскости в пространстве либо параллельны, либо пересекаются. Примеры в окружающем пространстве найти легко.
Если две плоскости имеют общую точку, то они пересекаются по прямой.
19.Перпендикуляр и наклонная. Теорема о трех перпендикулярах.
| ||
| О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если прямая, проведенная на плоскости черезоснование наклонной, перпендикулярна еепроекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. | 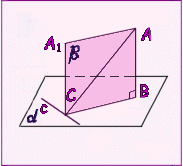 | |
20. Угол между прямой и плоскостью. Параллельность прямой и плоскости.
Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.
Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.
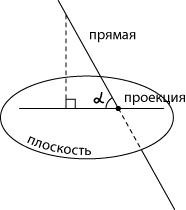
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.
Признаки параллельности прямой и плоскости:
1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Признаки параллельности плоскостей:
1) Если две пересекающиеся прямые одной плоскости cоответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
2) Если две плоскости перпендикулярны одной и той же прямой, то они параллельны.
21. Угол между плоскостями. Перпендикулярность двух плоскостей.
Угол, образованный этими лучами и есть линейный угол двугранного угла:
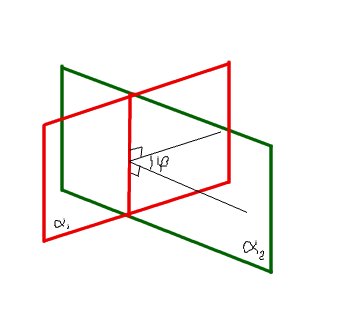 Величиной угла между плоскостями называется величинаменьшегодвугранного угла.
Величиной угла между плоскостями называется величинаменьшегодвугранного угла.
Пусть наши плоскости 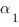 и
и 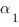 заданы уравнениями:
заданы уравнениями:
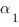 :
: 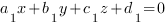
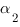 :
: 
Косинус угла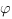 между плоскостями находится по такой формуле:
между плоскостями находится по такой формуле:
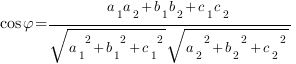
Две плоскости будут перпендикулярны друг к другу, если одна из них проходит через прямую, перпендикулярную другой плоскости (рис. 6.4).
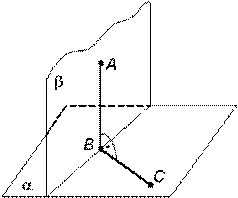
Рис 6.4
АВ 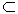 b, то есть АВ принадлежит плоскости b и АВ ^ плоскости a. Плоскость b ^ плоскости a.
b, то есть АВ принадлежит плоскости b и АВ ^ плоскости a. Плоскость b ^ плоскости a.
22.Понятие многогранника. Призма. Правильная призма.
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, назв многогранником. Тетраэдр и параллелепипед - примеры многогранников
Стороны граней называются рёбрами, а концы рёбер - вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Многогранники бывают выпуклые и невыпуклые. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 360o.
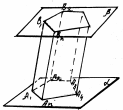 рис. 50 рис. 50 |
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые рёбра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае - наклонной. Высота прямой призмы равна ее боковому ребру.
Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани - равные прямоугольники.
Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы - сумма площадей ее боковых граней.
Sполн = Sбок + 2Sосн
Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
 2015-05-14
2015-05-14 4199
4199

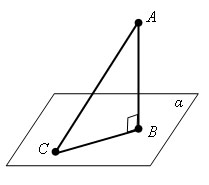 AB – перпендикуляр к плоскости α. AC – наклонная, CB – проекция. С – основание наклонной, B - основание перпендикуляра.
AB – перпендикуляр к плоскости α. AC – наклонная, CB – проекция. С – основание наклонной, B - основание перпендикуляра. 






