В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,
а, k, C - постоянные величины.
· 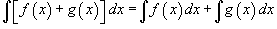
· 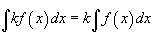
· 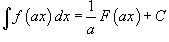
· 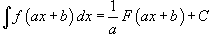
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.
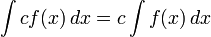
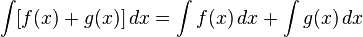
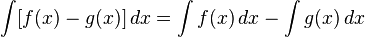
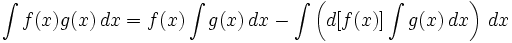
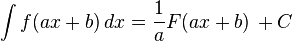
11. Методы интегрирования неопределённого интеграла.
Несомненно, основным методом нахождения первообразной функции является непосредственное интегрирование с использованием таблицы первообразных и свойств неопределенного интеграла. Все другие методы используются лишь для приведения исходного интеграла к табличному виду.
При интегрировании функций с иррациональностью вида 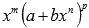 , где m, n, p – рациональные числа, важно правильно выбрать выражение для введения новой переменной. Смотрите рекомендации в разделе интегрирование иррациональных функций.
, где m, n, p – рациональные числа, важно правильно выбрать выражение для введения новой переменной. Смотрите рекомендации в разделе интегрирование иррациональных функций.
Очень часто метод подстановки используется при интегрировании тригонометрических функций. К примеру, использование универсальной тригонометрической подстановки позволяет преобразовать подынтегральное выражение к дробно рациональному виду.
Метод подстановки позволяет объяснить правило интегрирования 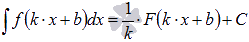 .
.
Вводим новую переменную 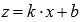 , тогда
, тогда
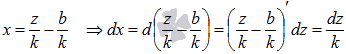
Подставляем полученные выражения в исходный интеграл:
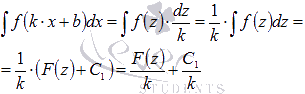
Если принять 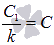 и вернуться к исходной переменной х, то получим
и вернуться к исходной переменной х, то получим
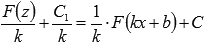
12.Определенный интеграл и его свойства.
Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если 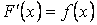 , то
, то
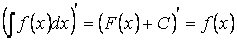
Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению
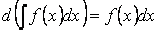
Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы
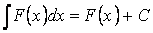
Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов
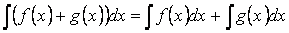
Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов
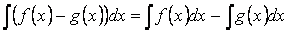
Свойство 6. Постоянный множитель можно выносить за знак интеграла
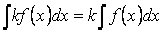
Свойство 7. Если
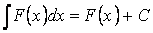
то

13.Методы интегрирования определённого интеграла. Пример.
1) 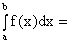
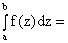
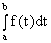 ;
;
2) 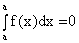 ;
;
3) 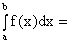 -
- 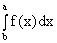 ;
;
4) 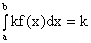
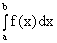 , (k = const, k∈ R);
, (k = const, k∈ R);
5) 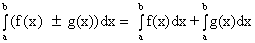 ;
;
6) 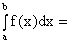
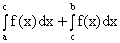 ;
;
7) 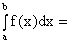 f(ξ)(b-a) (ξ∈a,b]).
f(ξ)(b-a) (ξ∈a,b]).
Пример 3.30. Вычислить ∫ dx/(x+2).
Решение. Обозначим t = x+2, тогда dx = dt, ∫dx/(x+2) = ∫dt/t = lnïtï+C =
= ln(ïx+2)ï+C.
14.Плошадь криволинейной трапеции.
Пусть на отрезке [а; b] оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [а; b] и прямыми х = а и х = b (рис. 1), называют криволинейной трапецией. Различные примеры криволинейных трапеций приведены на рисунках 1, а — д.
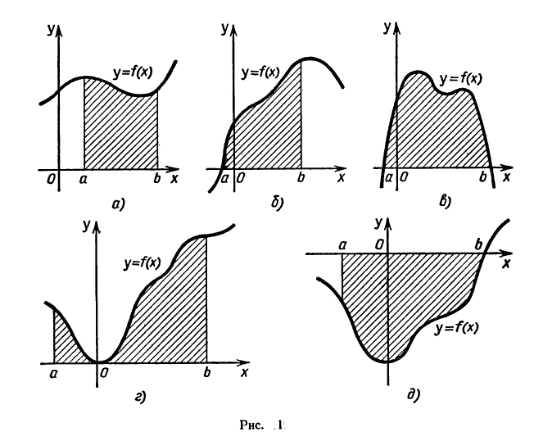
Для вычисления площадей криволинейных трапеций применяется следующая теорема:
Теорема. Если f — непрерывная и неотрицательная на отрезке [а; b] функция, a F — ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции (рис. 2) равна приращению первообразной на отрезке [а; b] т. е.
S=F(b)-F(a). (1)
15.Аксиомы стереометрии и следствия из них.
новные фигуры в пространстве: точки, прямые и плоскости.
 |  |  |
| рис. 1 | рис. 2 | рис. 3 |
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.
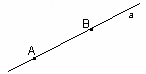
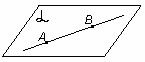
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
 | А   В В   (точки А, В, С лежат в плоскости (точки А, В, С лежат в плоскости  ) С ) С   |
| рис. 4 |
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
 | АB   Прямая АВ лежит в плоскости Прямая АВ лежит в плоскости  |
| рис. 5 |
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
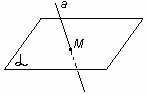 | а   = М Прямая а и плоскость = М Прямая а и плоскость  пересекаются в точке М. пересекаются в точке М. |
| рис. 6 |
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
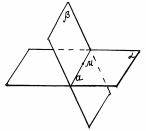 |    = a = a  и и  пересекаются по прямой а. пересекаются по прямой а. |
| рис. 7 |
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
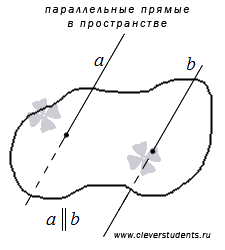
16. Взаимное расположение прямых в пространстве. Параллельность прямых в пространстве.
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
– прямые совпадают.
Две прямые на плоскости называются параллельными, если они не имеют общих точек.

Определение.
Две прямые в трехмерном пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
17. Взаимные расположения прямой и плоскости в пространстве. Параллельность прямой и плоскости.
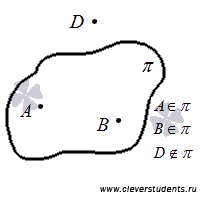
К примеру, если точка А не лежит в плоскости 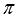 , то используют краткую запись
, то используют краткую запись 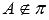 .
.
 2015-05-14
2015-05-14 1162
1162
