2015-05-14
695
Основная идея метода состоит в том, что будем рассматривать некоторые постоянные l1, l2, …, ln, которые называются множителями Лагранжа и строим следующую функцию.
Составляется функция Лагранжа:
L (x1, …, xn, l1, …, ln) = f (x1, …, xn) + li (qi – qi(x1, …, xn)).
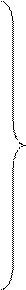Вычисляется частная производная:
/
Lx1 = 0
/
Lx2 = 0
…
…
…
/
Lxn = 0
/
Ll1 = 0
/
Ll2 = 0
…
/
Lln = 0
Находится решение данной системы.
Решение подвергается дополнительным условиям с использованием достаточных условий экстремума. Например, если функция состоит из двух переменных: Z = f (x;y), то находится следующий определитель:
// //
Zxx Zxy
D = // //
Zyx Zyy
Если D< 0, то экстремум не существует, если D > 0, то существует, причем если:
// //
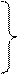
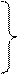Zxx > 0 c min Zxx < 0 cmax
// //
Zyy > 0 Zyy < 0
Пример. По плану производства продукции предприятию необходимо изготовить 180 изделий. Эти изделия могут быть изготовлены двумя технологическими способами. Обозначим х1 – количество изделий первым способом; х2 – количество изделий вторым способом.
Затраты при первом способе равны 2
|
|
|
2 4х1 + х1;
втором способе - 8х2 + х2.
Определить, сколько изделий в каждом из способов следует изготовить, чтобы затраты были минимальными.
Решение. Составляем модель: С = 4х1 + х1 + 8х2 + х2 Òmin.
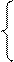х1 + х2 = 180
х1 > = 0
x2 > = 0
2 2
1. L (x1, x2, l) = 4x1 + x1 + 8x2 + x2 + l(180 – x1 – x2)
 |
2. Lx1 = 4 + 2x1 - l = 0
/
Lx2 = 8 + 2x2 - l = 0.
3. –4 + 2x1 – 2x2 = 0 (:2)
-2 + x1 – x2 = 0
180 – x1 – x2 = 0
182 – 2x1 = 0
x1 = 91 шт. (1 – способом)
-2 + 91 – х2 = 0
х2 = 89 шт. (2 – способом).
// /
4. сх1х1 = (4 + 2х1)х1 = 2
// /
сх2х2 = (8 + 2х2)х2 = 2 //
// / 2 0 ex1x1 > 0
сх1х2 = (4 + 2х1)х2 = 0 D = 0 2 = 4 > 0 c min.
ex2x2 > 0
Ответ: производство, выполняет первым способом 91 шт., вторым способом 89 шт. При том будут минимальные затраты.
