/ // (n)
DY – выражение F(x,y,y,y,…,y) = 0.
Определение. Порядком DY называется наивысший порядок производной (n(.
Определение. Линейным DY n – порядка называется уравнение вида:
(n) (n-1)
у + а1(х)у + … + аn(х)у = b(x), где а1(х),…,аn(x), b(x) - известные функции,
y - искомая функция.
 Если b(x) = 0, то уравнение называется неоднородным, если b(x) = 0 называется однородным.
Если b(x) = 0, то уравнение называется неоднородным, если b(x) = 0 называется однородным.
Определение. Решением DY n – порядка называется всякая функция
у = j (х) при подстановке которой тождество становится верным.
Пример. Найти решение уравнения / 2
у –3х = 0;
/ 2
у = 3х
y = 3xdx = x + C - общее решение DY,
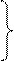 у = х + 5
у = х + 5
+1 частное решение DY
+2
Дифференциальные уравнения с разделяющимися переменными.
 |
Пусть дано выражение: f1(x) * j 2 (y)dx + f2(x) j 1(y)dy = 0:j 2 (y)*f(x) =
= f1(x) * j 2 (y)dx/j 2(y)* f2(x) + f2(x) * j 1 (y)dy/ j 2(y)* f2(x) = 0
f 1(x)dx/f2(x) + j 1(y)dy/j 2 (y).
Чтобы решить данное полученное уравнение необходимо интегрировать каждую часть:
ò f 1(x)dx/fx(x) + ò j 1(y)dy/ j 2(y) = ò 0.



 Пример. Найти общее решение DY.
Пример. Найти общее решение DY.
 2 2 2 2
2 2 2 2



 х * 1 - y * dx + y * 1 –x * dy = 0: (1- у * 1 – х)
х * 1 - y * dx + y * 1 –x * dy = 0: (1- у * 1 – х)



 2 2 2 2
2 2 2 2



 х dx / 1 – x + y dy/ 1 – y = 0 ò x dx/ 1 – x + ò y dy/ 1 –y = ò 0.
х dx / 1 – x + y dy/ 1 – y = 0 ò x dx/ 1 – x + ò y dy/ 1 –y = ò 0.
Метод подстановки.
 2 2
2 2
 1 – х = t p = 1 - y
1 – х = t p = 1 - y

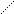



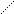
x = 1 – t y = 1 - p
-2x dx = dt -2y dy = dp
dx = dt/-2x dy = dp/-2y
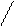


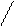







 ò 1 – t dt/ -2 * 1 – t * t + ò 1 – p dp/-2 * 1 – p * p = C
ò 1 – t dt/ -2 * 1 – t * t + ò 1 – p dp/-2 * 1 – p * p = C
-1/2 ò dt / t – 1/2 ò dp/ p = C
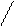

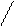
 1/2 1/2
1/2 1/2

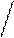

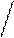 -1/ 2 *t /1/2 – 1/2 * p / 1/2 = C - t – p = C
-1/ 2 *t /1/2 – 1/2 * p / 1/2 = C - t – p = C

 2 2
2 2
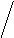

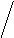
 - 1 – x – 1 - y = C
- 1 – x – 1 - y = C

 2 2
2 2

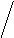 1 – y = – 1 - x – C
1 – y = – 1 - x – C
 2 2 2
2 2 2
1 – y = (- 1 – x – C)
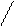

 2 2
2 2

 y = m 1 – (- 1 – x – C) - общее решение дифференциального уранения.
y = m 1 – (- 1 – x – C) - общее решение дифференциального уранения.
Пример. Найти общее решение DY.
 xy dx + y dy = 0
xy dx + y dy = 0
x dx + dy = 0: у
ò x dx + ò dy = ò 0
2 2
x /2 + y = c, y = c – x /2 – общее решение дифференциального уравнения.
Перечень основных понятий: Первообразная функция F(x). Неопределенный интеграл. Метод подстановки. Интегрирование по частям. Определенный интеграл. Метод вычисления определенного интеграла: формула Ньютона - Лейбница. Метод подстановки интегрирования по частям. Вычисление площади фигуры. Дифференциальные уравнения. Дифференциальные уравнения с разделяющимися переменными.
Ключевые моменты: Первообразная функция F(x). Неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Основные методы интегрирования. Метод подстановки. Интегрирование по частям. Определенный интеграл. Использование определенного интеграла в экономической задаче. Геометрическая интерпретация. Свойства определения интеграла. Метод вычисления определенного интеграла: формула Ньютона- Лейбница. Метод подстановки интегрирования по частям. Вычисление площади фигуры. Использование определенного интеграла в экономической задаче. Дифференциальные уравнения. Дифференциальные уравнения с разделяющимися переменными.
Вопросы к самопроверке:
1. Первообразная функция F(x). Неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов.
2. Основные методы интегрирования. Метод подстановки. Интегрирование по частям.
3. Определенный интеграл. Использование определенного интеграла в экономической задаче. Геометрическая интерпретация.
4. Свойства определения интеграла.
5. Метод вычисления определенного интеграла: формула Ньютона- Лейбница.
6. Метод подстановки интегрирования по частям.
7. Вычисление площади фигуры.
8. Использование определенного интеграла в экономической задаче.
9. Дифференциальные уравнения.
10. Дифференциальные уравнения с разделяющимися переменными.
Рекомендуемая литература:
1. Кремер Б.А. Высшая математика для экономистов. Учебник для ВУЗов. М.: Банки и бирж, ЮНИТИ, 1998 г. С. 251-354.
2. Зорич В.А. Математический анализ, Т.1. М., “Наука”, 1981.
3. Ильин В.А., Позняк Э.Г. Основы математического анализа. М., “Наука”, 1980.
4. Кудрявцев Л.Д. Математический анализ, Т.1, М., “Высшая школа”, 1981.
5. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1, М., “Наука”, 1980.
6. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М., “Наука”, 1979.
7. Берман Г.Н. Сборник задач и упражнений по математическому анализу.
Ряды
 2015-05-14
2015-05-14 434
434







