Пример. Исследовать на сходимость обощенный гармонический ряд

Исследовать на сходимость обощенный гармонический ряд .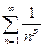

Решение. Члены ряда составляют монотонно убывающую последовательность .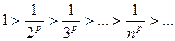

Следовательно, функцией f(x) будет .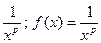

Рассмотрим 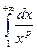и .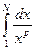

;

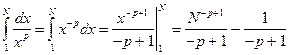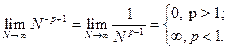
Тогда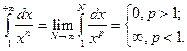

Если р=1, то имеем 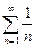- гармонический ряд, расходимость которого доказана ранее.

Ряд 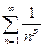сходится при р>1 и расходится при р  1.

Знакопеременные ряды

Прежде чем рассматривать ряды с членами произвольных знаков, расмотрим их частный случай, а именно ряды, члены которых имеют чередующиеся знаки, такие ряды называются знакочередующимися.

Знакочередующийся ряд, если первый член положителен, можно записать в виде:

U₁ - U₂ + U₃ - U₄ +... + (-1)ⁿ⁺¹U_n +..., где U_n>0, n=1, 2, 3,....