Доказательство. Поскольку любая скобка в этой сумме больше нуля, то последовательность {S2n} возрастающая

Построим S_2n = U₁ - U₂ + U₃ - U₄ +... + U_2n-1 - U_2n = (U₁ - U₂) +

+ (U₃ - U₄) +... + (U_2n-1 - U_2n).

Поскольку любая скобка в этой сумме больше нуля, то последовательность {S_2n} возрастающая. Докажем, что она ограниченная. Для этого представим S_2n следующим образом:

S_2n = U₁ - [(U₂ - U₃) + (U₄ - U₅) +... + (U_2n-2 - U_2n-1) + U_2n] < U₁

Итак, последовательность {S_2n} монотонно возрастающая, ограниченная и, следовательно, сходящаяся. Пусть .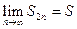

Чтобы доказать сходимость ряда, нужно доказать еще, что последовательность частичных сумм нечетного числа членов этого ряда также сходится и имеет предел, равный S.

Так как S_2n+1 = S_2n + U_2n+1 и U_2n+1  0 (по условию), то

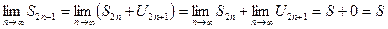
Заметим, что для суммы S ряда (1) справедливо соотношение 0<S<U₁. Действительно, частные суммы четных номеров S_2n приближаются к сумме S, возрастая, следовательно, S>S_2n при любом n. Кроме того, S_2n>0 (n=1, 2,...), а значит и S>0. Частичные суммы нечетных номеров S_2n+1 можно записать в виде:

S_2n+1 = U₁ - (U₂ - U₃) -... - (U_2n - U_2n+1).

Отсюда видно, что последовательность {S_2n+1} монотонно убывающая и что S_2n+1<U₁ при любом n. Так как S<S_2n+1 при любом n, то, следовательно, S<U₁. Суммируя сказанное, получаем: 0<S<U₁.

Рассмотрим теперь остаток ряда, умноженный на (-1)ⁿ

(-1)ⁿ r _n= U_n+1 - U_n+2 +...

Это ряд. По доказанному ряд сходится и его сумма не превосходит первого члена, то есть r_n < U_n+1.

Теорема доказана.