Теорема. Если сходится ряд (8.2), то сходится и ряд (8.1)

Если сходится ряд (8.2), то сходится и ряд (8.1).

Доказательство сразу получается из принципа сходимости: неравенство

|U_n+1 + U_n+2 +... + U_n+m|  |U_n+1| + |U_n+2| +... + |U_n+m|

показывает, что если условие сходимости выполняется для ряда (8.2), то оно тем более выполняется для ряда (8.1).

Можно рассуждать иначе. Из положительных членов ряда (8.1), перенумеровав их по порядку, составим ряд

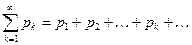(P),

так же поступим с отрицательными членами и составим ряд из их абсолютных величин

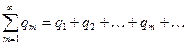(Q)

Сколько бы членов того или другого ряда ни взять, все они содержатся среди членов сходящегося ряда (8.2), и для всех частичных сумм Р_к и Q_m выполняются неравенства

Р_к  S*; Q_m  S*.

Так что оба ряда (Р) и (Q) сходятся, обозначим их суммы соответсвенно, через Р и Q.

Если взять n членов ряда (А), то в их составе окажется k положительных и m отрицательных, так что

S_n = P_k - Q_m. (8.3)

Здесь номера k и m зависят от n. Если в ряде (8.1) как положительных, так и отрицательных членов бесчисленное множество, то при n одновременно k и m.

Переходя в равенстве (8.3) к пределу, приходим снова к заключению о сходимости ряда (8.1), причем его сумма оказывается равной

S = P - Q.

Можно сказать, что при сделанных предположениях сумма данного ряда равна разности между суммой ряда, составленного из одних положительных его членов, и суммой ряда, составленного из абсолютных величин отрицательных членов.

Если ряд (8.1) сходится вместе с рядом (8.2), составленным из абсолютных величин его членов, то про ряд (8.1) говорят, что он абсолютно сходится.

Если ряд (8.1) сходится и ряд (8.2) расходится, то ряд (8.1) называют условно сходящимся.

Между свойствами абсолютно и условно сходящихся рядов имеется глубокое различие.