Доказательство. Заметим, что вследствие сходимости ряда его общий член стремится к нулю: ; поэтому абсолютные величины

Заметим, что вследствие сходимости ряда 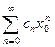его общий член стремится к нулю: 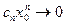; поэтому абсолютные величины

членов этого ряда, начиная с некоторого n=N, меньше любого наперед заданного числа >0. Так как имеется конечное число членов ряда с номерами, меньшими N, то абсолютные величины этих членов ограничены некоторым числов М (в качестве М можно взять максимальную абсолютную величину членов ряда с этими номерами или , если оно больше). Следовательно, абсолютные величины всех членов ряда не превосходят числа М.

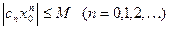. (9.2)

Представим ряд (9.1) в виде

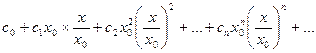
и составим ряд из абсолютных величин его членов:

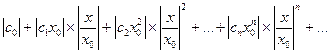(9.3)

Сравним его с рядом, составленным из членов геометрической прогрессии

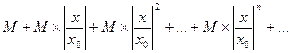. (9.4)

Если |x|<|x₀|, то для этого ряда 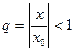, а поэтому он сходится. Так как при любом n имеют места неравенства (9.2), то члены ряда (9.3) не превосходят соответсвующих членов ряда (9.4). Члены этих рядов положительны, и, значит, в силу признака сравнения ряд (9.3) также сходится. Следовательно, и ряд (9.1) сходится, и притом абсолютно, при любом |x|<|x₀|.