Пример. Для любого х, начиная с достаточно большого n, будет

Рассмотрим ряд .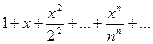

Для любого х, начиная с достаточно большого n, будет 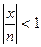. Так как 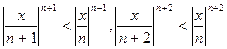и т. д., то, начиная с

номера n, члены ряда по абсолютной величине будут меньше членов сходящейся геометрической прогрессии. Следовательно, при любом х ряд сходится.

Область сходимости ряда может состоять более, чем из одной точки оси Ох, причем есть точки оси, не принадлежащие области сходимости.

Например, ряд 1 + х + х² +... + хⁿ +..., представляющий геометрическую прогрессию со знаменателем х, сходится при |x|<1 и расходится при |x|1.

Из теоремы Абеля и ее следствия получаем, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости. Совершенно ясно, что точки сходимости будут целиком заполнять некоторый интервал с центром в начале координат.

Таким образом, можно сказать, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число R, что для всех х, по модулю меньших R (|x|<R), ряд абсолютно сходится, а для всех х, по модулю больших R (|x|>R), ряд расходится.

Что касается значений х = R и х = - R, то здесь могут быть различные возможности: ряд может сходится в обеих точках, или только в одной из них, или ни в одной. При этом ряд может сходиться как абсолютно, так и условно.