Доказательство. Составим ряд из абсолютных величин членов ряда (9.1)

Составим ряд из абсолютных величин членов ряда (9.1)

|c₀| + |c₁ x| + |c₂ x²| +... + |c_n xⁿ| +.... (9.5)

Найдем отношение 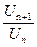для этого ряда:

,

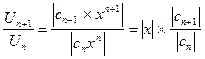а затем предел его при n:

.

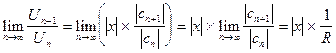Здесь множитель |x| вынесен за знак предела, как не зависящий от n, и введено обозначение

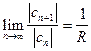, (9.6)

если этот предел существует и не равен нулю. Согласно признаку Даламбера, ряд (9.5) сходится, если 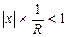, откуда |x|<R.

Отсюда следует, что ряд (9.1) сходится, и притом абсолютно, при значениях |x|<R. Согласно тому же признаку Даламбера, ряд (9.5) расходится, если 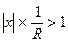, или |x|>R. Однако в этом случае из признака Даламбера следует, что члены ряда (9.5) не стремятся к нулю. Тогда при n не стремятся к нулю и члены ряда (9.1), а потому и он расходится при значениях |x|>R. Следовательно, согласно определению, число R - радиус сходимости степенного ряда (9.1). Из соотношения (9.6) получим

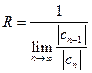, т. е. 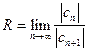. (9.7)

Приведем примеры:

1⁰ Найдем радиус сходимости ряда .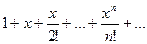

.

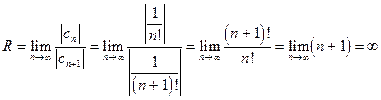2⁰ Найти область сходимости степенного ряда

.

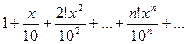Найдем отношение

.

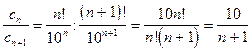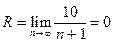, т. е. ряд сходится только при х=0 и расходится при остальных значениях х.

3⁰ Найти область сходимости степенного ряда:

.

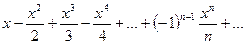Здесь 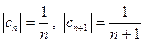, т. е. .

.

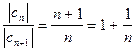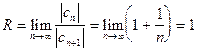Исследуем сходимость ряда на концах интервала сходимости.

При х=1 имеем ряд 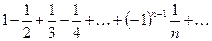, он сходится по теореме Лейбница.

При х=-1 имеем ряд 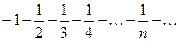, который расходится как произведение расходящегося гармонического ряда на -1. Следовательно, областью сходимости служит полуинтервал (-1; 1].

4⁰ Найти область сходимости степенного ряда

,

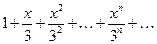Найдем радиус сходимости ряда

.

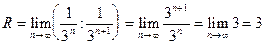Исследуем сходимость ряда при значениях х= 3. Подставив их в в данный ряд, соответственно получим 1 + 1 + 1 +... + 1 + 1 +...;

1 - 1 + 1 -... + (-1)ⁿ +.... Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при n). На обоих концах интервала сходимости данный ряд расходится, а область его сходимости (-3; 3).

Формула радиуса сходимости степенного ряда получена в предположении, что все коэффиценты членов ряда, начиная с некоторого, отличны от нуля. Применение формулы (9.7) допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать или с помощью признаков Даламбера, Коши, или же сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.