Найти сумму степенного ряда
1 - х + х2 -... + (-1)n xn +....
Это ряд, составленный из членов геометрической прогрессии, у которой b1=1, q= -x. Следовательно, его сумма есть функция 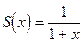 . Ряд сходится, если |x|<1. Поэтому равенство
. Ряд сходится, если |x|<1. Поэтому равенство
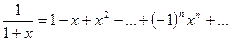
справедливо лишь для значений х(-1; 1), хотя функция 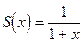 определена для всех значений х, кроме х= -1.
определена для всех значений х, кроме х= -1.
Можно доказать, что сумма степенного ряда S(x) непрерывна и дифференцируема на любом отрезке [a, b] внутри интервала сходимости.
Равенство (10.2), справедливое в интервале сходимости степенного ряда, называют разложением S(x) в степенной ряд.
Для степенных рядов справедливы следующие утверждения:
 2015-05-14
2015-05-14 1182
1182








