Элементарная теория дейтрона

Обычно, это изучение задачи двух тел (дейтрон). Это объясняется тем, что

1. она математически не очень сложна;

2. решение этой задачи позволит предсказать природу ядерных сил, хотя ядерные силы не аддитивны.

Рассмотрим простое ядро, состоящее из протона и нейтрона и несмотря на то, что одна из частиц, входящих в состав – нейтрон – нестабильная частица, сам дейтрон характеризуется бесконечным временем жизни. Важной характеристикой дейтрона является энергия связи, равная 2,23 МэВ. Дейтрон обладает спином S=1 и магнитным моментом, равным , квадрупольным моментом 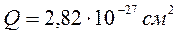. Если сравнить квадрупольный момент с поперечными размерами системы, то видно, что он мал, откуда следует, что основное состояние дейтрона почти сферически симметрично. Следовательно, ядерное взаимодействие между протоном и нейтроном почти центральное. Итак, нашей задачей является система (р, р), (n, n) или (n, р). В (р, р), (n, n) – нет связанного состояния, а в (n, р) - есть одно связанное состояние – дейтрон. Будем считать, что потенциал ядерного взаимодействия – это потенциал притяжения и в первом приближении не зависит ни от спина, ни от скорости частицы, а является только функцией расстояния частицы. Из этого вытекает, что на вид потенциала накладываются небольшие ограничения, т.е. ядерные силы не критичны к самому виду потенциала, необходимо только, чтобы потенциал быстро убывал с расстоянием, т.е. нужен маленький радиус действия и большая величина на расстояниях меньших 1Фм.

Такому условию отвечают следующие виды потенциала:

1. 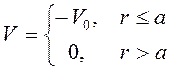− прямоугольная потенциальная яма;

2. 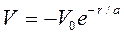– экспоненциальный потенциал;

3. 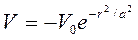– Гауссовский потенциал;

4. 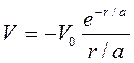− потенциал Юкава.

Рассмотрим подробно прямоугольную потенциальную яму. Тогда уравнение Шредингера для двух частиц, находящихся в потенциальной яме будет:

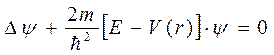(8.1),

где

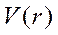− потенциал ядерных сил;

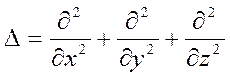− оператор Лапласа;

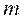−приведенная масса, определяемая из выражения:

(8.2)

Заменив массу, получим

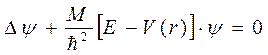
Из всего оператора выберем зависимость только от расстояния
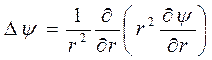(8.3),

подставим 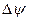в уравнение Шредингера и получим

.

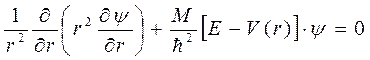Перейдем к новым переменным, заменив 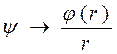, тогда 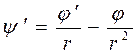. Вычислим

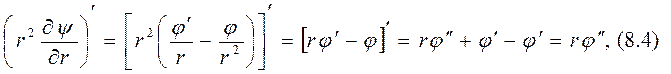Подставим новые переменные в уравнение Шредингера

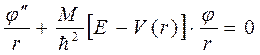, (8.5)

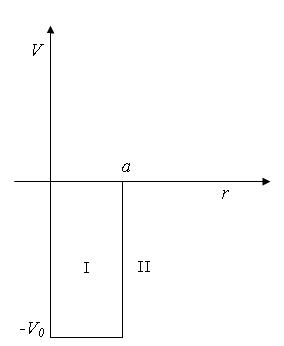В качестве потенциала дейтрона используем прямоугольную потенциальную яму (рис.1)

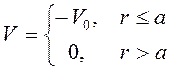
Энергия внутри ядра ~ -V₀

вне ядра ~ 0

Прямоугольная потенциальная яма.

Уравнение позволяет найти лишь один параметр, относящийся к потенциалу: при известном V(r) дает собственные значения Е₀ свободного состояния, равное энергии связи дейтрона или при известном Е позволяет найти V₀ и ширину ямы, не определяя сами эти величины. Это мы и сделаем. Очевидно, что устойчивые состояния существуют при условии, что Е=-Е_0. Тогда для первой области

I.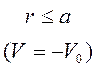

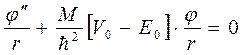
II. .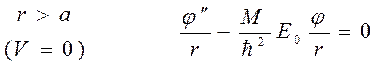

Эти уравнения и нужно решить.

Введем обозначения:

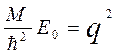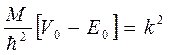и , где 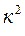, 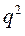положительные числа.

Тогда уравнение примет вид:

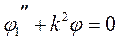
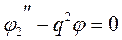
Нас интересуют только те значения энергии Е, когда частица не может выйти из потенциальной ямы, т.е. V(r)>>E₀

Ищем решение уравнения Шредингера в виде:

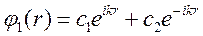
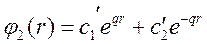
Т.к. 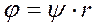, то граничное условие будет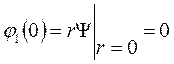

Используя это соотношение получим С₁ и С₂

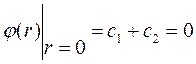, т.е. ,

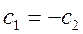Следовательно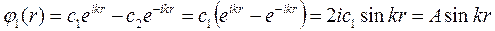

т.к.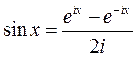

Итак .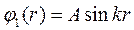

Используя второе граничное условие (при r → ∞) получим 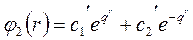при r → ∞

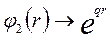
Но такое решение физически неприемлемо и чтобы получить решение, согласное с физическим смыслом нужно предположить, что 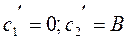. Тогда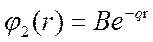

Мы видим, что, первому решению соответствуют квантованные значения энергии, а второму непрерывные.

Для определения постоянных А и В нужно вспомнить, что решение уравнения Шредингера должно быть непрерывными вместе со своими производными, что означает, что переходы между 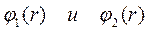, 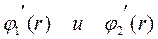должны быть непрерывны

Используя эти условия, решение примет вид:

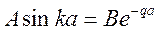
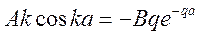
Решая совместно эти уравнения, получим ;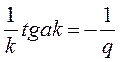

Отсюда получим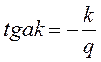

Вспомним, что 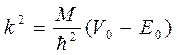и . Подставив эти значения, получим 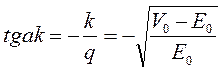, т.е при известной глубине потенциальной ямы 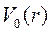можно получить энергию дейтрона 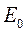. Очевидно, что 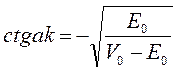и если учесть, что малая величина энергии связи указывает на то, что 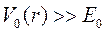, то отбросив в знаменателе 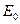и получим 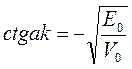, следовательно, 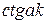равен малому отрицательному числу. Отрицательный знак указывает на то, что 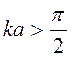, поэтому можно считать, что .

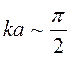Это и есть условие существования уровней в яме и тогда

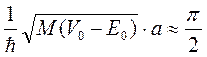
Учитывая, что 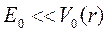получим, что 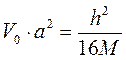, где

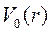- глубина ямы;

а – ширина ямы;

Т.е. яма может быть как глубокой и узкой, так и широкой и мелкой.

О глубине ямы мы до конца ответа не имеем, данное условие определяет минимальную глубину потенциальной ямы, чтобы в ней существовало связанное состояние, и это состояние получено при условии 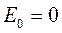. Нам известно, что 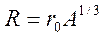, где 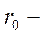радиус действия ядерных сил; Подставив значение 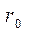можно оценить радиус дейтрона 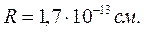; считая, что 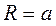и зная массу М можно оценить глубину ямы . Следовательно, яма узкая и глубокая и нормальный уровень ее лежит вблизи края ямы, что объясняет малую устойчивость дейтрона. Особый интерес представляет случай, когда 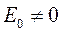. Тогда 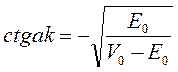, т.е это есть трансцендентное уравнение, которое рассматривается графически.

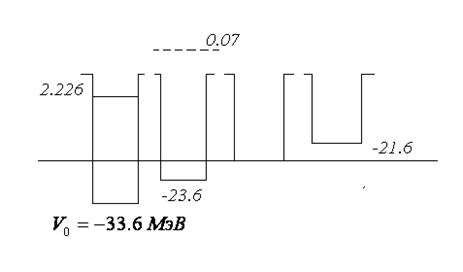
Из рисунка видно, что уровень, соответствующий энергии связи 2,226 МэВ в яме шириной 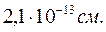может существовать, только если глубина ее 33,6 МэВ. Для уровня 0,07 достаточна глубина 23,6 МэВ. Если глубина меньше чем 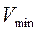, то уровень поднимается выше края ямы, т.е. связанное состояние невозможно. В этом случае считается, что система имеет виртуальный уровень, который может проявляться при рассеянии электронов при соответствующих энергиях. Отметим, что при оценке 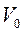мы считали, что 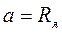. Однако волновая функция не равна нулю, при 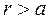она убывает по закону 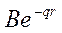. Поэтому ширина ямы 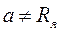, но можно указать радиус сферы, где частицы дейтрона проводят основную часть времени; т.к. при 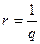функция уменьшается в е раз, то 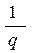можно принять за радиус дейтрона. Следовательно, .

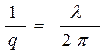Если приравнять их и учесть, что Е₀=2,23 МэВ, то можно получить радиус дейтрона 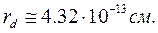Т.о. оценка показывает, что радиус действия ядерных сил значительно меньше радиуса дейтрона, Следовательно, частицы ядра часть времени проводят вне потенциальной ямы, в области .

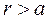Итак

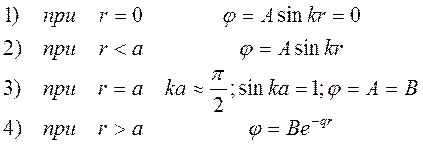
Следовательно, у дейтрона есть только один уровень, он не может находиться в возбужденном состоянии. Если же ему сообщить энергию 2,226 МэВ, то дейтрон разлетится на протон и нейтрон. При сообщении меньшей энергии, он поглощает ее и остается в нормальном состоянии. Итак, при рассмотрении ядерных сил мы оценили потенциал взаимодействия, сделали ряд предположений, использовали квантовую механику и оценили ядерные силы, действующие при нуклон – нуклонном взаимодействии. Мы получили, что потенциал имеет сложный вид и с учетом поправок содержит 6 слагаемых.

Наряду с силами, приводящие к полному обмену координат, могут существовать силы, связные с обменом пространственных или спиновых координат в отдельности. Обычно, различные обменные силы рассматриваются по именам их исследователей, которые впервые их рассмотрели. Различают:

1. Силы Майорана – это обменные силы, учитывающие перестановку пространственных координат.

2. Силы Бартлета – это обменные силы, учитывающие обмен спиновых координат;

3. Силы Гейзенберга – это обменные силы, учитывающие обмен как пространственных так и спиновых координат;

4. Силы Вигнера – это необменные силы, описывающиеся обычным центральным потенциалом.

Из анализа тензорного и обменного взаимодействия следует, что возможен один лишь вид обменных тензорных сил – Силы Майорана. Т.о. потенциал ядерного взаимодействия между двумя нуклонами с учетом обменного и тензорного характера в самом общем виде будет

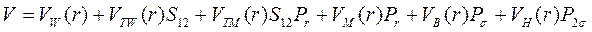
где,

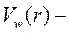обменный потенциал;

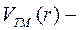тензорный потенциал;

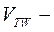потенциал Вигнера;

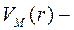Центральные силы Майорана;

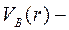силы Вигнера;

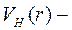силы Гейзенберга.

Следовательно, выражение, полученное, с требованием инвариантности относительно пространственных превращений, отражений, симметрии относительно осей координат в самом общем виде содержит 6 функций. Практически вопрос о нахождении функции 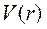остается открытым.