Геометрическое определение вероятности

Иногда задачи Т.В. легче решать, представив их геометрически.

Пусть отрезок l составляет часть отрезка L. На отрезок наугад (случайным образом) поставлена точка. Если предположить, что вероятность попадания точки на отрезок пропорциональна длине этого отрезка, то вероятность попадания точки на отрезок l равна отношению длин отрезков: .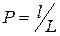

Пусть плоская область g составляет часть плоской области G. Внутрь области наугад поставлена точка. Если предположить, что вероятность попадания точки в плоскую область пропорциональна площади этой области, то вероятность попадания точки в область g равна отношению площадей этих областей: .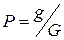

Аналогично для пространственных областей v и V.

Вероятность попадания точки в пространственную область v равна отношению объемов этих областей: .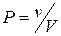

Пр. 1. Внутри эллипса 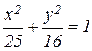расположен круг 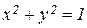. Найти вероятность попадания точки в кольцо, ограниченное эллипсом и кругом.

Найдем вероятность события А={попадание точки в кольцо}.

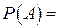
Пр. 2. В квадрат с вершинами (0,0), (0,1), (1,0), (1,1) наудачу поставлена точка 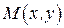. Найти вероятности событий:

, , .

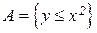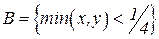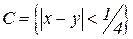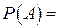
В={или x, или y меньше }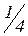

, .

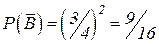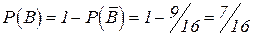Найдем площадь области :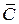

, .

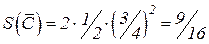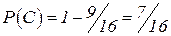Эта задача является примером известной задачи про встречу:

двое договорились встретиться между 12⁰⁰ и 13⁰⁰ и ждать друг друга 15 минут (т.е. 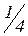часа). Здесь найдена вероятность встречи ().

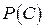Теорема 2 сложения вероятностей совместных событий:

Вероятность появления хотя бы одного из двух совместных событи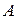й и 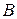равна сумме вероятностей этих событий без вероятности их совместного появления:

,

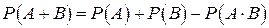Для случая трех событий формула имеет вид:

.

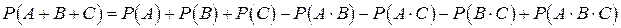Пр. 3. …

Два события называют независимыми, если вероятность одного из них не зависит от появления или непоявления другого.

Пр. 4. …

Теорема 3 умножения вероятностей независимых событий:

Вероятность совместного появления двух (или нескольких) независимых событий равна произведению вероятностей этих событий:

,

.

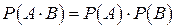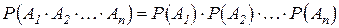Пр. 5. В 1-м ящике 2 белых и 10 синих шаров, во 2-м ящике – 8 белых и 4 синих шара. Из каждого ящика взяли по шару. Найти вероятность того, что оба шара белые.

Рассмотрим события: 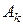={появление белого шара из k-го ящика}, k=1,2.

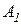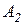События и - независимые.

, , .

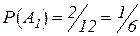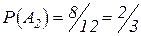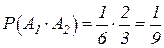Лекция 5.