Построили график каждого временного ряда.
а) График временного ряда для количества дичи:
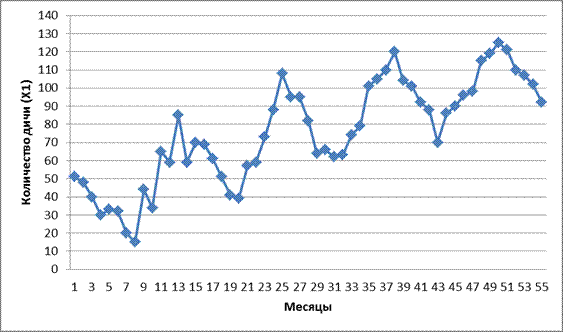
В среднем количество убитых уток увеличивается (т.к. левая часть графика ниже правой, что говорит о наличии тренда);
Ярко прослеживаются сезонные колебания, так как функция в 4х точках достигает своего максимума в среднем через 12 месяцев и своего минимума в среднем через 12 месяцев, что говорит о сезонности.
б) график временного ряда для веса Робинзона:
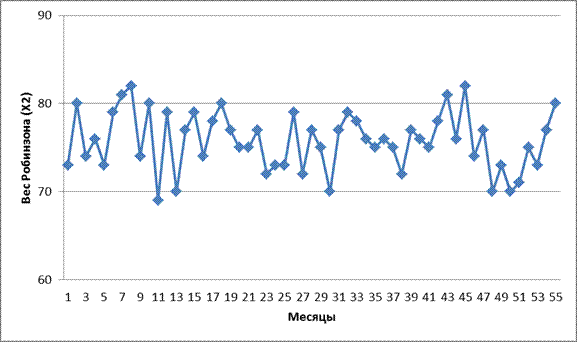
При динамике веса выражены сезонные колебания, а роста среднего значения веса в течении 5 лет не прослеживается.
Провели первичный статистический анализ временных рядов, включая вычисление среднего значения, меры разброса. Сделали соответствующие выводы.
1) Х1ср = 75,69091
Х2ср = 75,74545
Значит в среднем Робинзон добывал ~76 дичи, а его вес в среднем составлял ~76 кг.
2) 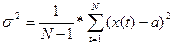 - дисперсия временного ряда
- дисперсия временного ряда
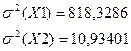
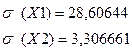
3. Проверим гипотезу Н0 и ее альтернативу Н1:
H0(0): 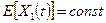
H0(1): 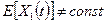
H1(0): 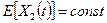
H1(1): 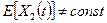
Проверка гипотез с помощью критерия серий:
| Критерий серий | |||||||||
| t | X1 | t | X1 | t | X2 | t | X2 | ||
| - | - | ||||||||
| - | + | ||||||||
| - | - | ||||||||
| - | |||||||||
| - | - | ||||||||
| - | + | ||||||||
| - | + | ||||||||
| - | + | ||||||||
| - | - | ||||||||
| - | + | ||||||||
| - | - | ||||||||
| - | + | ||||||||
| + | - | ||||||||
| + | + | ||||||||
| - | + | ||||||||
| - | - | ||||||||
| - | + | ||||||||
| - | + | ||||||||
| - | + | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | + | ||||||||
| - | - | ||||||||
| + | - | ||||||||
| + | - | ||||||||
| + | + | ||||||||
| + | - | ||||||||
| + | + | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | + | ||||||||
| - | + | ||||||||
| - | + | ||||||||
| + | - | ||||||||
| + | |||||||||
| + | - | ||||||||
| + | - | ||||||||
| + | + | ||||||||
| + | |||||||||
| + | - | ||||||||
| + | + | ||||||||
| - | + | ||||||||
| + | |||||||||
| + | + | ||||||||
| + | - | ||||||||
| + | + | ||||||||
| + | - | ||||||||
| + | - | ||||||||
| + | - | ||||||||
| + | - | ||||||||
| + | - | ||||||||
| + | - | ||||||||
| + | + | ||||||||
| + | + |
Найдем статистики 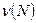 и
и 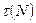 и проверим неравенства:
и проверим неравенства:
1) 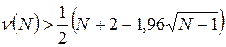
2) 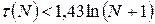 .
.
Если хоть одно из них не выполняются, то гипотеза 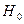 отвергается с вероятностью ошибки a, такой, что 0,05 < a < 0,0975, что подтверждается наличие зависящей от времени неслучайной составляющей в
отвергается с вероятностью ошибки a, такой, что 0,05 < a < 0,0975, что подтверждается наличие зависящей от времени неслучайной составляющей в 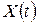 .
.
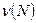 -количество серий;
-количество серий;
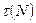 - максимальное количество элементов с серии;
- максимальное количество элементов с серии;
· 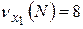
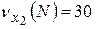
· 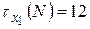
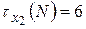
1) 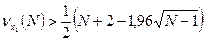 → не выполняется (8<21,3);
→ не выполняется (8<21,3);
2) 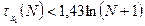 → не выполняется (12>5,8);
→ не выполняется (12>5,8);
1) 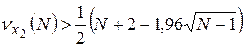 → выполняется (30>21,3)
→ выполняется (30>21,3)
2) 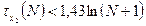 → выполняется (6>5,8)
→ выполняется (6>5,8)
Следовательно, гипотезы 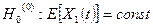 и
и 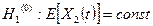 отвергаются.
отвергаются.
Проверка гипотезы с помощью критерия "восходящих" и "нисходящих" серий:
| Критерий восходящих и нисходящих серий | |||||
| Х1 | Х2 | ||||
| + | + | ||||
| - | + | ||||
| - | - | ||||
| - | + | ||||
| + | - | ||||
| - | + | ||||
| - | + | ||||
| - | + | ||||
| + | - | ||||
| - | + | ||||
| + | - | ||||
| - | + | ||||
| + | - | ||||
| + | + | ||||
| - | + | ||||
| - | - | ||||
| - | + | ||||
| - | + | ||||
| - | - | ||||
| - | - | ||||
| + | |||||
| + | + | ||||
| + | - | ||||
| + | + | ||||
| + | |||||
| - | + | ||||
| - | - | ||||
| - | + | ||||
| - | - | ||||
| + | - | ||||
| - | + | ||||
| + | + | ||||
| + | - | ||||
| + | - | ||||
| + | - | ||||
| + | + | ||||
| + | - | ||||
| + | - | ||||
| - | + | ||||
| - | - | ||||
| - | - | ||||
| - | + | ||||
| - | + | ||||
| + | - | ||||
| + | + | ||||
| + | - | ||||
| + | + | ||||
| + | - | ||||
| + | + | ||||
| + | - | ||||
| - | + | ||||
| - | + | ||||
| - | - | ||||
| - | + | ||||
| - | + | ||||
| v1(N)кр= | 30,30636 | v1(N)кр= | 30,30636 | ||
| t1(N)кр= | t1(N)кр= | ||||
| v1(N)= | отв | v1(N)= | не отв | ||
| t1(N)= | отв | t1(N)= | не отв | ||
| отвергается | не отвергается |
Найдем статистики 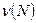 и
и 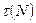 . Если не выполняется хоть одно из неравенств:
. Если не выполняется хоть одно из неравенств:
1) 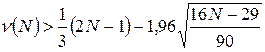 ;
;
2) 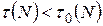 ,
,
то гипотеза 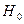 отвергается.
отвергается.
Найдем:
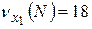
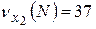
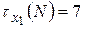
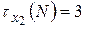
1) 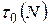 =6;
=6;
2) 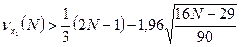 не выполняется (18<30,3);
не выполняется (18<30,3);
1) 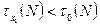 не выполняется (7>6);
не выполняется (7>6);
2) 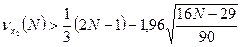 выполняется (37>30,3);
выполняется (37>30,3);
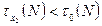 выполняется (3<6)
выполняется (3<6)
Следовательно, гипотеза 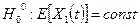 отвергается, а гипотеза
отвергается, а гипотеза 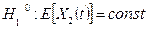 не отвергается.
не отвергается.
Задание 4. Построить уравнение для неслучайных компонент, присутствие которых в модели было доказано. Провести сравнительный анализ моделей А, В и С, выбирая типы моделей по таблице 2. Обосновать по результатам эконометрического анализа выбор наилучшей модели.
Построим уравнения для неслучайных компонент временного ряда 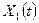 :
:
Шаг 1: Используя метод скользящего среднего, выровняем исходный ряд 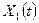 . Для этого суммируем элементы ряда последовательно за каждые 12 месяцев со сдвигом на один момент времени и, разделив полученные суммы на 12, найдем скользящие средние. Для приведения в соответствие с фактическими моментами времени найдем центрированные скользящие средние. Получим
. Для этого суммируем элементы ряда последовательно за каждые 12 месяцев со сдвигом на один момент времени и, разделив полученные суммы на 12, найдем скользящие средние. Для приведения в соответствие с фактическими моментами времени найдем центрированные скользящие средние. Получим
| скользящие средние за год | центророванные скользящие средние |
| 39,33333 | |
| 42,16667 | 40,75 |
| 45,58333 | 43,875 |
| 48,08333 | 46,83333 |
| 51,33333 | 49,70833 |
| 53,66667 | 52,5 |
| 55,25 | 54,45833 |
| 56,125 | |
| 58,91667 | 57,95833 |
| 59,45833 | |
| 62,08333 | 61,04167 |
| 62,75 | 62,41667 |
| 65,16667 | 63,95833 |
| 67,08333 | 66,125 |
| 67,58333 | 67,33333 |
| 69,66667 | 68,625 |
| 70,75 | 70,20833 |
| 70,875 | |
| 72,25 | 71,625 |
| 73,125 | |
| 77,41667 | 76,70833 |
| 79,08333 | 78,25 |
| 81,41667 | 80,25 |
| 82,83333 | 82,125 |
| 82,91667 | |
| 85,08333 | 84,04167 |
| 85,83333 | 85,45833 |
| 87,41667 | 86,625 |
| 89,75 | 88,58333 |
| 91,58333 | 90,66667 |
| 92,25 | 91,91667 |
| 94,16667 | 93,20833 |
| 95,5 | 94,83333 |
| 96,91667 | 96,20833 |
| 96,66667 | 96,79167 |
| 97,5 | 97,08333 |
| 98,25 | 97,875 |
| 98,66667 | 98,45833 |
| 100,0833 | 99,375 |
| 100,8333 | 100,4583 |
| 102,0833 | 101,4583 |
| 103,25 | 102,6667 |
| 105,0833 | 104,1667 |
Шаг 2: Найдем оценки сезонной компоненты S, которые определяются как разность между фактическими элементами ряда и центрированными скользящими средними.
Получим
| Шаг 2 | ||||||||||||
| k= | 0,10 | |||||||||||
| год\мес. | ||||||||||||
| -20,75 | -27,88 | -2,83 | -15,71 | 12,50 | 4,54 | |||||||
| 28,88 | 31,04 | 10,54 | 7,96 | -1,42 | -12,96 | -25,13 | -28,33 | -11,63 | -11,21 | 2,13 | 16,38 | |
| 34,88 | 20,00 | 18,29 | 3,75 | -16,25 | -16,13 | -20,92 | -21,04 | -11,46 | -7,63 | 12,42 | 14,33 | |
| 18,08 | 26,79 | 9,17 | 4,79 | -4,79 | -9,08 | -27,88 | -12,46 | -9,38 | -4,46 | -3,46 | 12,33 | |
| 14,83 | ||||||||||||
| Siсредн | 24,17 | 25,94 | 12,67 | 5,50 | -7,49 | -12,72 | -23,67 | -22,43 | -8,82 | -9,75 | 5,90 | 11,90 |
| Si | 24,07 | 25,84 | 12,57 | 5,40 | -7,59 | -12,82 | -23,77 | -22,53 | -8,92 | -9,85 | 5,80 | 11,80 |
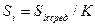 , где
, где 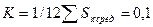
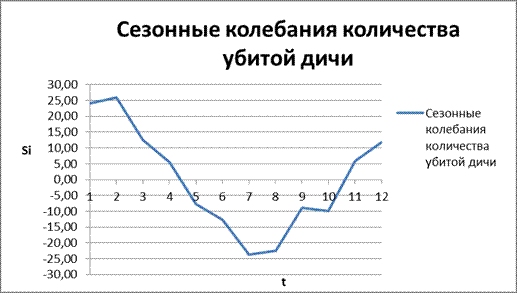
График сезонности
Выводы по графику:
На графике видно, что Робинзону лучше всего ходить на охоту в начале года (с 1го по 5й месяцы), а также в конце года (с середины 10го месяца по 12й).
В эти периоды ему следует запасаться на середину года (с 5го по 10е месяцы).
Шаг 3: Исключим влияние сезонной компоненты, вычитая ее значения из каждого элемента временного ряда. Получим 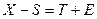 .
.
Шаг 4: Используя регрессионный анализ, проведем аналитическое выравнивание ряда X-S. Построим три модели:
1) 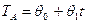 , 2)
, 2) 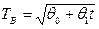 , 3)
, 3) 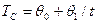 . Найдем оценки параметров
. Найдем оценки параметров 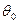 и
и 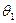 для каждого уравнения с помощью МНК.
для каждого уравнения с помощью МНК.
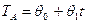 СНУ:
СНУ:
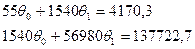
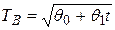
Делаем замену 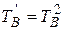
Получим 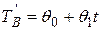 СНУ:
СНУ:
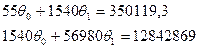
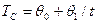
Делаем замену 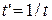
Получим 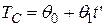 СНУ:
СНУ:
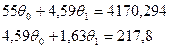
Получим три уравнения
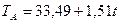 ,
, 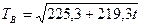 и
и 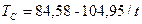
Построим соответствующие графики
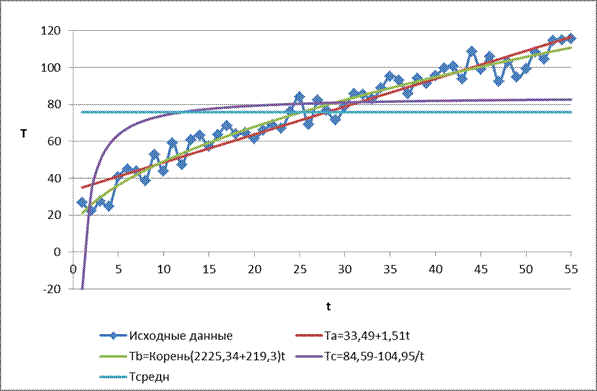
Исходя из анализа графика, видим, что наиболее точно зависимость количества убитой дичи от времени описывают модели 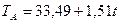 и
и
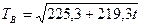
Проверим значимость найденных моделей
Если 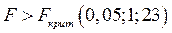 , то гипотеза
, то гипотеза 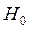 отвергается с вероятностью 0,95.
отвергается с вероятностью 0,95.
Если 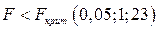 , то гипотеза
, то гипотеза 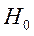 не отвергается с вероятностью 0,95.
не отвергается с вероятностью 0,95.
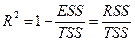
Для 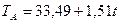
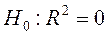
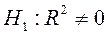
R2= 0,928
F= 685,31>Fкрит =4,02, следовательно, 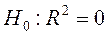 отвергается, что говорит о значимости нашей модели, и ее можно использовать для прогнозирования
отвергается, что говорит о значимости нашей модели, и ее можно использовать для прогнозирования
Для 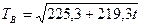
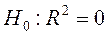
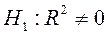
R2= 0,952
F= 1106,08>Fкрит =4,02, следовательно, 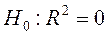 отвергается, что говорит о значимости нашей модели, и ее можно использовать для прогнозирования.
отвергается, что говорит о значимости нашей модели, и ее можно использовать для прогнозирования.
Для 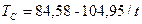
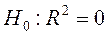
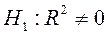
R2= 0,4
F= 35,72>Fкрит =4,02, следовательно, 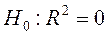 отвергается, что говорит о значимости нашей модели, и ее можно использовать для прогнозирования.
отвергается, что говорит о значимости нашей модели, и ее можно использовать для прогнозирования.
Сравнивая эти полученные значения R2, делаем вывод, что лучшая модель 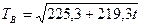 , так как R2= 0,952 в данном случае наибольшее, следовательно, эта модель лучше всего описывает зависимость количества убитой дичи от времени.
, так как R2= 0,952 в данном случае наибольшее, следовательно, эта модель лучше всего описывает зависимость количества убитой дичи от времени.
5. Выводы:
После построения графика сделали следующие выводы:
· в среднем количество убитых уток увеличивается; прослеживаются сезонные колебания;
· при динамике веса отсутствуют сезонные колебания, и рост среднего значения веса не прослеживается.
· Провели первичный статистический анализ временных рядов, включая вычисление среднего значения, меры разброса. Таким образом, среднее отклонение количества добытых уток от среднего значения равно 28,6, а среднее отклонение веса 3,3. Следовательно колебания количества добытой дичи в течение времени весьма значительно, а вот колебание веса Робинзона невелико.
· Построили график сезонности на год проживания Робинзона на острове, чтобы дать рекомендации Робинзону в какой период ему лучше охотиться.
· Построили 3 модели, и в дальнейшем вывели, что модели А и В наиболее точно описывает исходные данные (количество убитой дичи).
 2015-05-18
2015-05-18 1148
1148
