Теорема Гаусса-Маркова

Применение метода наименьших квадратов (МНК) к оценке параметров линейной модели не всегда позволяет получить состоятельные оценки (Напоминаю: состоятельные оценки - обладающие свойством несмещённости при больших объёмах выборки).

Для получения состоятельных оценок необходимо, чтобы они удовлетворяли ряду условий, эти условия сформулированы в теореме Гаусса-Маркова.

Теорема Гаусса-Маркова формулирует условия, при которых МНК позволяет получить наилучшие оценки параметров линейной модели множественной регрессии.

К.Ф Гаусс (1777-1855) – разработка МНК

А.А. Марков (1856-1922) – сформулировал условия, при которых МНК позволяет получить состоятельные оценки.

Сформулируем постановку задачи:

Имеем:

1) спецификацию модели в виде линейного уравнения множественной регрессии

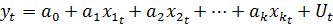(«уравнение звёздочка» *)

2) выборку из n наблюдений

Значения переменных в каждом наблюдении связаны между собой по правилу (*)

Следовательно,

(5.17)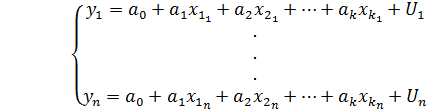

Система уравнений (5.17) называется системой уравнений наблюдений или схемой Гаусса-Маркова.

В компактной (матричной) записи эта система имеет вид

В матрице Х в первом столбце единицы появляются только в тех случаях, когда спецификация содержит свободный параметр .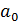

Если этот параметр отсутствует, то и в матрице Х этот столбец отсутствует.

Перейдём к задаче.

Необходимо

1. найти значение состоятельных оценок параметров моделей

2. оценку ошибки случайного возмущения

3. оценку наилучшего прогноза с помощью модели (5.17)

4. оценку ошибки прогноза эндогенных переменных

Предпосылки теоремы Гаусса-Маркова следующие:

1) математическое ожидание случайных возмущений во всех наблюдениях равно нулю

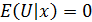(5.20)

2) дисперсия случайных возмущений во всех наблюдениях одинакова и равна const. И свойство однородности случайных возмущений

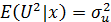(5.21)

3) ковариация между парами случайных возмущений в наблюдениях равна нулю

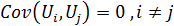(5.22)

→ отсутствие автоковариации случайных возмущений

Неравенство нулю (≠0) есть автоковариация

4) ковариация между вектором-регрессором и вектором случайных возмущений равна нулю → регрессоры и случайные возмущения НЕ зависят друг от друга

.

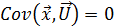(далее непонятная неведомая фигня)

Если матрица X неколлинеарна, т.е нет ни одного столбца, который можно было бы приставить в виде линейной комбинации других столбцов, то

1) наилучшая оценка вектора параметров линейной модели множественной регрессии вычисляется по правилу

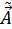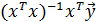= (5.24) - она (оценка) соответствует МНК

2) значение несмещённых оценок параметров

Ковариационная матрица параметров модели вычисляется

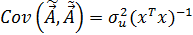(5.25)

3) дисперсия случайного возмущения равна:

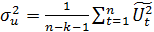(5.26)

4) наилучший прогноз по модели (5.17) в точке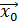

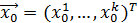
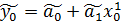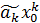+…+ (5.27)

5) оценка ошибки прогноза эндогенной переменной равна

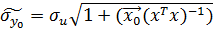
Билет №31