2015-05-18
1171
(5.8)
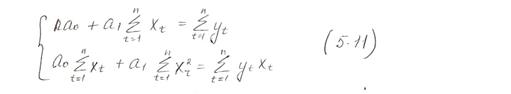
(5.11) - Система нормальных уравнений для определения оценок параметров модели (5.8).
Систему уравнений (5.11) можно решить методом исключения переменных. Для этого достаточно выразить параметр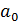 
через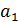 
, подставив его во второе уравнение системы, откуда получен 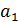, затем уже 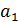подставить в первое уравнение.
В итоге:
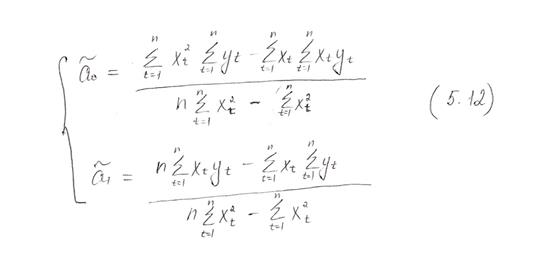
Выражение (5.12) позволяет по известным значениям наблюдений переменных x и y вычислить оценки параметров модели парной регрессии.
Известно, что ковариация -
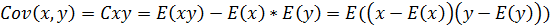(5.13)
- числовая характеристика взаимосвязи пары случайных переменных x и y.
(взаимосвязь нефункциональная)
Дисперсия является частным случаем ковариации
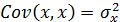
Из (5.13) следует, что для вычисления ковариации нужно знать закон распределения случайных переменных x и y → P(x,y). Если он неизвестен, то ковариацию можно оценить по выборке из генеральной совокупности
XY, x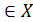 
, y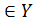 
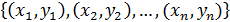
X = {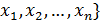 
Y = {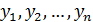 
}
Оценкой ковариации служит величина выборочная:
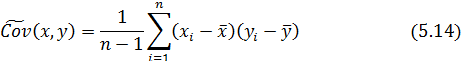
в частном случае
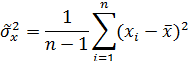
С учётом (5.14), преобразовав (5.12) получим оценку параметра 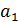, т.е.
Преобразуем (5.15)
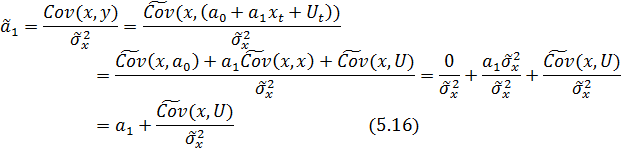
Таким образом, оценка параметра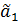 
отличается от его [параметра 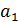] истинного значения на величину отношения оценки ковариации регрессора и остатка к оценке дисперсии.
Отсюда видно, что, несмотря на то что случайное возмущение непосредственно не участвует в вычислении значения оценок параметра, оно существенно влияет на их [оценок параметров] качество, а именно, если случайное возмущение коррелирует с регрессором, то значение оценки становится смещённым. (Напоминаю: оценка параметров закона распределения называется несмещённой, если её математическое ожидание совпадает со значением параметра: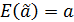 
.)
Корреля́ция (от лат. correlatio — соотношение, взаимосвязь), корреляционная зависимость — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин
Коэфф-т корреляции
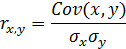
Билет 29
