Структура лагов по Койку: Частные случаи (модель с неполной корректировкой и адаптивных ожиданий)

Эндогенные иэкзогенные переменные редко включаются в модель в один и тот же моментвремени. Решения, которые должны принять участники экономики, требуют t, необходимого для их воплощения в жизнь. ЭМ в которой экзогенные переменные входят с учетом запаздывания во времени, носят названия лаговых.

МЛР с запаздывающей во времени экзогенной переменной

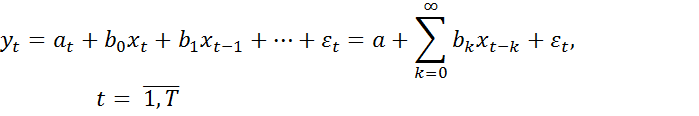
Для физической реализуемости динамической модели требуется выполнение условия сходимости следующего ряда: 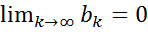. На практике применяется модель с конечным числом запаздываний, являющаяся частным случаем предыдущей.

1) Геометрическая лаговая структура (Койка). Пусть все параметры b_kубывают с ростом k по геометрической прогрессии со знаменателем q(0<q<1)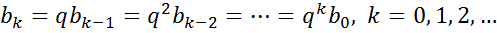

Тогда рассмотренная модель примет упрощенный вид:

.

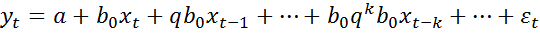Окончательно нормализованный вид модели: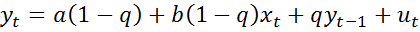

В этой модели необходимо оценить лишь три неизвестных параметра (a,b и q) вместо 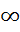, но => появление сериальной корреляции случайной переменной u_t. Тесты проверки на сериальную корреляцию: Тест h-Дарбина и Множественный критерий Лагранжа.

Модель адаптивных ожиданий.

Обозначим через 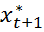ожидаемое (в момент t) будущее значение переменной x_t. Значение величины y_tопр этим ожидаемым значением:

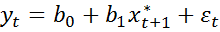(1) – долгосрочная ф-я адаптивных ожиданий

Гипотеза адаптивных ожиданий предпо­лагает, что ожидания пересматриваются в некоторой пропорции от разницы между наблюденным знач и про­гнозом переменной х на предыдущем шаге: 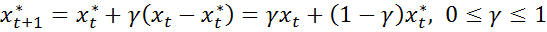(2)

Если ү=0, то ситуация не изменится, если 1 - ситуация будет близка к прогнозной. Напр. фирма при­нимает решение об V производимой в период tпродукции y_tдо того, как известна цена x_t+1. Поскольку цена x_t+1не из­вестна в период t, то решение принимается на основе ожидаемого значения 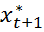–яв-сявзвеш средним наблюдаемой цены х и ожидаемой цены х* в период t.

Если выразить 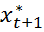через x_tиз (2), введя оператор запаздывания:

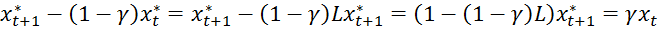
и подставив в (1)

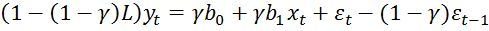или

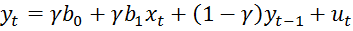
Эта модель (краткосрочная ф-я адаптивных ожиданий) совпадает с моделью Койка. Модель включает только фактические знач переменных, поэтому их можно определить с помощью стандартных стат методов.

Модель с неполной корректировкой.

В отличие от пред модели эмпирически ненаблюдаемой переменной яв-ся результативный признак. Общий вид этой модели сле­дующий:

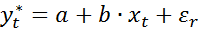(3) долгосрочная ф-я неполной корректировки

Формирование ожиданий экономических агентов относи­тельно значений 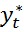происходит по следующей схеме:

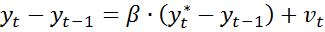, где .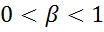

В этой модели предполагается, что абсолютное изменение фактических уровней результата есть некоторая доля его ожидае­мого абсолютного изменения. Параметр 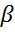этой модели называ­ют корректирующим коэффициентом. Чем ближе величина 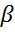к 1, тем в большей степени реальная динамика показателя отвечает ожиданиям экономических агентов. Чем ближе 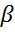к 0, тем менее реальное изменение показателя соответствует его ожидаемому изменению. При 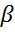= 0 значение результативного признака явля­ется константой, на которую ожидания агентов не оказывают ни­какого воздействия.Запишем гипотезу о формировании у' в виде:

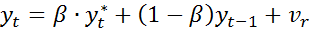(4) где 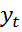фактическое знач результата текущего периода.

Подставим уравнение (3) в (4). Получим:

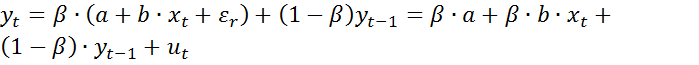(5)где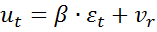

Соотношение (5) есть основное уравнение модели непол­ной корректировки. Его называют краткосрочной функцией мо­дели. Включает только фактические значения переменных. Зная оцен­ки параметров этого уравнения, можно найти 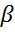. Затем найти a, b.